| Citation: |
Jianlong Ren, Qiming Liu, Jiangyan He. THE COLLISION-AVOIDING FINITE-TIME FLOCKING OF A CUCKER-SMALE MODEL WITH PINNING CONTROL AND EXTERNAL PERTURBATION[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1503-1519. doi: 10.11948/20240273
|
THE COLLISION-AVOIDING FINITE-TIME FLOCKING OF A CUCKER-SMALE MODEL WITH PINNING CONTROL AND EXTERNAL PERTURBATION
-
Abstract
The Cucker-Smale model plays a vital role in analyzing flocking behavior. To investigate the impact of pinning control and external perturbation on finite-time flocking behavior, a modified Cucker-Smale model that incorporates these factors is proposed in this paper. Initially, by imposing appropriate restrictions on external perturbation, the system can achieve finite-time flocking, and the upper bound of settling time is derived explicitly. Subsequently, a new sufficient condition is given to ensure collision-avoiding during the flocking process. The results show that the convergence time depends on control parameters and the convergence speed of the perturbation. Lastly, numerical simulations are provided to illustrate the derived results.
-
-
References
[1] H. Ahn, Asymptotic flocking of the relativistic Cucker-Smale model with time delay, Netw. Heterog. Media., 2023, 18(1), 29–47. [2] S. M. Ahn, H. Choi, S.-Y. Ha and H. Lee, On collision-avoiding initial configurations to Cucker-Smale type flocking models, Commun. Math. Sci., 2012, 10(2), 625–643. doi: 10.4310/CMS.2012.v10.n2.a10 [3] S. M. Ahn and S.-Y. Ha, Stochastic flocking dynamics of the Cucker-Smale model with multiplicative white noises, J. Math. Phys., 2010, 51(10), 103301. doi: 10.1063/1.3496895 [4] H.-O. Bae, Y.-P. Choi, S.-Y. Ha and M.-J. Kang, Asymptotic flocking dynamics of Cucker-Smale particles immersed in compressible fluids, Discrete. Cont. Dyn.-A., 2014, 34(11), 4419–4458. doi: 10.3934/dcds.2014.34.4419 [5] J. Byeon, S.-Y. Ha and J. Kim, Asymptotic flocking dynamics of a relativistic Cucker-Smale flock under singular communications, J. Math. Phys., 2022, 63(1), 012702. doi: 10.1063/5.0062745 [6] M. Chen, X. Wang and Y. Liu, Collision-free flocking for a time-delay system, Discrete. Cont. Dyn.-B., 2021, 26(2), 1223–1241. [7] T. Chen, X. Liu and W. Lu, Pinning complex networks by a single controller, IEEE. T. Circuits.-I., 2007, 54(6), 1317–1326. doi: 10.1109/TCSI.2007.895383 [8] J. Cheng, L. Ru, X. Wang and Y. Liu, Collision-avoidance, aggregation and velocity-matching in a Cucker-Smale-type model, Appl. Math. Lett., 2022, 123, 107611. doi: 10.1016/j.aml.2021.107611 [9] J. Cheng, X. Wang and Y. Liu, A singular inter-particle force in Cucker-Smale model to avoid collisions, Appl. Anal., 2023, 102(8), 2380–2388. doi: 10.1080/00036811.2022.2027380 [10] Y.-P. Choi, S.-Y. Ha and J. Kim, Propagation of regularity and finite-time collisions for the thermomechanical Cucker-Smale model with a singular communication, Netw. Heterog. Media., 2018, 13(3), 379–407. doi: 10.3934/nhm.2018017 [11] F. Cucker and J.-G. Dong, Avoiding collisions in flocks, IEEE. T. Automat. Contr., 2010, 55(5), 1238–1243. doi: 10.1109/TAC.2010.2042355 [12] F. Cucker and J.-G. Dong, A general collision-avoiding flocking framework, IEEE. T. Automat. Contr., 2011, 56(5), 1124–1129. doi: 10.1109/TAC.2011.2107113 [13] F. Cucker and J.-G. Dong, A conditional, collision-avoiding, model for swarming, Discrete. Cont. Dyn.-A., 2014, 34(3), 1009–1020. doi: 10.3934/dcds.2014.34.1009 [14] F. Cucker and S. Smale, Emergent behavior in flocks, IEEE. T. Automat. Contr., 2007, 52(5), 852–862. doi: 10.1109/TAC.2007.895842 [15] R. Erban, J. Haskovec and Y. Sun, A cucker-smale model with noise and delay, SIAM. J. Appl. Math., 2016, 76(4), 1535–1557. doi: 10.1137/15M1030467 [16] S.-Y. Ha, T. Ha and J.-H. Kim, Emergent behavior of a Cucker-Smale type particle model with nonlinear velocity couplings, IEEE. T. Automat. Contr., 2010, 55(7), 1679–1683. doi: 10.1109/TAC.2010.2046113 [17] S.-Y. Ha, K. Lee and D. Levy, Emergence of time-asymptotic flocking in a stochastic Cucker-Smale system, Commun. Math. Sci., 2009, 7(2), 453–469. doi: 10.4310/CMS.2009.v7.n2.a9 [18] S.-Y. Ha, Q. Xiao and X. Zhang, Emergent dynamics of Cucker-Smale particles under the effects of random communication and incompressible fluids, J. Diff. Eqs., 2018, 264(7), 4669–4706. doi: 10.1016/j.jde.2017.12.020 [19] G. H. Hardy, J. E. Littlewood and G. Pólya, Inequalities, Cambridge University Press, 1952. [20] X. Li, X. Wang and G. Chen, Pinning a complex dynamical network to its equilibrium, IEEE. T. Circuits.-I., 2004, 51(10), 2074–2087. doi: 10.1109/TCSI.2004.835655 [21] C.-B. Lian, G.-L. Hou, B. Ge and K. Zhou, Multi-cluster flocking behavior for a class of Cucker-Smale model with a perturbation, J. Appl. Anal. Comput., 2021, 11(4), 1825–1851. [22] H. Liu, X. Wang, X. Li and Y. Liu, Finite-time flocking and collision avoidance for second-order multi-agent systems, Int. J. Syst. Sci., 2020, 51(1), 102–115. doi: 10.1080/00207721.2019.1701133 [23] Z. Liu, Y. Liu and X. Wang, Emergence of time-asymptotic flocking for a general Cucker-Smale-type model with distributed time delays, Math. Method. Appl. Sci., 2020, 43(15), 8657–8668. doi: 10.1002/mma.6525 [24] L. Ru, X. Li, Y. Liu and X. Wang, Finite-time flocking of Cucker-Smale model with unknown intrinsic dynamics, Discrete. Cont. Dyn.-B., 2023, 28(6), 3680–3696. doi: 10.3934/dcdsb.2022237 [25] Y. Shen and X. Xia, Semi-global finite-time observers for nonlinear systems, Automatica, 2008, 44(12), 3152–3156. doi: 10.1016/j.automatica.2008.05.015 [26] Y. Sun, W. Li, H. Shi, D. Zhao and S. Azaele, Finite-time and fixed-time consensus of multiagent networks with pinning control and noise perturbation, SIAM. J. Appl. Math., 2019, 79(1), 111–130. doi: 10.1137/18M1174143 [27] T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Novel type of phase transition in a system of self-driven particles, Phys. Rev. Lett., 1995, 75(6), 1226. doi: 10.1103/PhysRevLett.75.1226 [28] L. Wang and F. Xiao, Finite-time consensus problems for networks of dynamic agents, IEEE. T. Automat. Contr., 2010, 55(4), 950–955. doi: 10.1109/TAC.2010.2041610 [29] Q. Wang, S. Ge and L. Jia, Pinning control of complex network by a single controller, J. Softw., 2012, 7(10), 2258–2262. [30] X. F. Wang and G. Chen, Pinning control of scale-free dynamical networks, Physica. A., 2002, 310(3–4), 521–531. doi: 10.1016/S0378-4371(02)00772-0 [31] X. Yin, D. Yue and Z. Chen, Asymptotic behavior and collision avoidance in the Cucker-Smale model, IEEE. T. Automat. Contr., 2019, 65(7), 3112–3119. [32] F. Zeng, X. Xue and Y. Zhu, Critical exponent for Cucker-Smale model under group-hierarchical multi-leadership, Appl. Math. Lett., 2023, 136, 108452. doi: 10.1016/j.aml.2022.108452 [33] X. Zhang, H. Dai, L. Zhao, D. Zhao and Y. Sun, Collision avoiding finite-time and fixed-time flocking of Cucker-Smale systems with pinning control, Int. J. Control., 2022, 95(8), 2045–2055. doi: 10.1080/00207179.2021.1892194 [34] R. Zhao, Q. Liu and H. Zhang, Flocking and collision avoidance problem of a singular Cucker-Smale model with external perturbations, Physica. A., 2022, 590, 126718. doi: 10.1016/j.physa.2021.126718 -
-
Figures(7) / Tables(1)
Export File
Citation
Jianlong Ren, Qiming Liu, Jiangyan He. THE COLLISION-AVOIDING FINITE-TIME FLOCKING OF A CUCKER-SMALE MODEL WITH PINNING CONTROL AND EXTERNAL PERTURBATION[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1503-1519. doi: 10.11948/20240273
Format
Content
DownLoad:
-
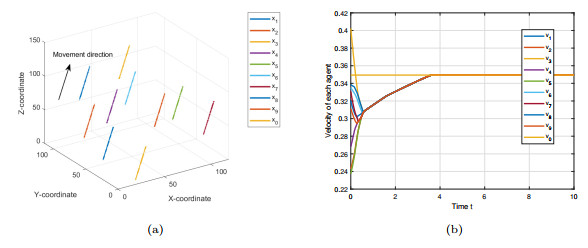
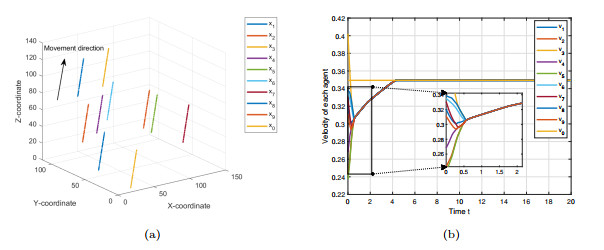
Figure 1.
The flocking without external perturbation.
-
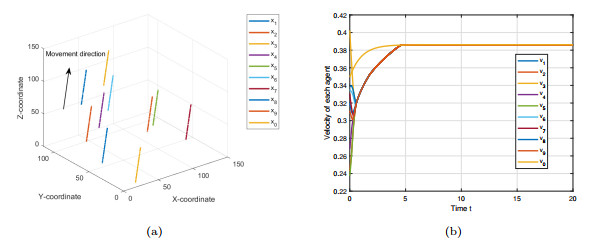
Figure 2.
The flocking with the first type of external perturbation.
-
Figure 3.
The flocking with the second type of external perturbation.
-
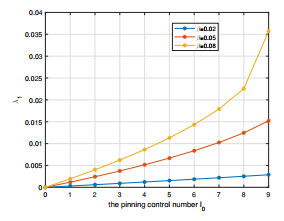
Figure 4.
The eigenvalue
$ \lambda_1 $ $ l_0 $ $ \beta $ -
Figure 5.
The flocking for different control gain
$ \beta $ -
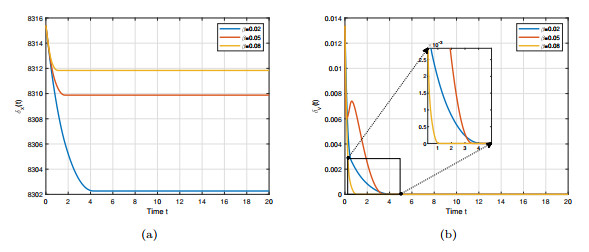
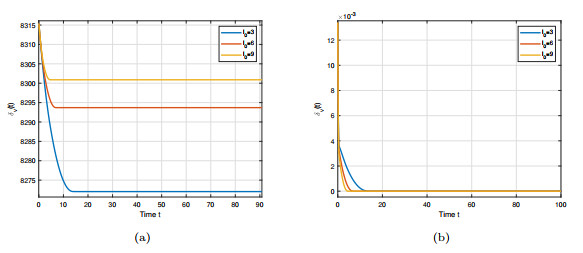
Figure 6.
The flocking with different
$ l_0 $ -
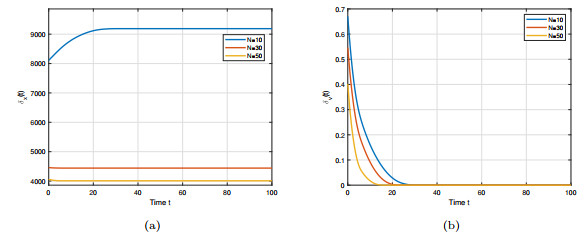
Figure 7.
The flocking with different
$ N $