| Citation: |
Litao Zhang, Haochen Zhao, Guangxu Zhu, Xiaojing Zhang. THE MODIFIED DOUBLE SHIFT-SPLITTING PRECONDITIONER FOR NONSYMMETRIC GENERALIZED SADDLE POINT PROBLEMS FROM THE TIME-HARMONIC MAXWELL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1520-1535. doi: 10.11948/20240279
|
THE MODIFIED DOUBLE SHIFT-SPLITTING PRECONDITIONER FOR NONSYMMETRIC GENERALIZED SADDLE POINT PROBLEMS FROM THE TIME-HARMONIC MAXWELL EQUATIONS
-
Abstract
Recently, Fan, Zhu and Zheng [Computational and Applied Mathematics, 37(3), 3256-3266] proposed a generalized double shift-splitting (GDSS) preconditioner induced by a new matrix splitting method for nonsymmetric generalized saddle point problems, and gave the corresponding theoretical analysis and numerical experiments. In this paper, based on the generalized double shift-splitting (GDSS) preconditioner, we generalize the GDSS algorithms and further present the modified double shift-splitting (MDSS) preconditioner for nonsymmetric generalized saddle point problems having a nonsymmetric positive definite (1,1)-block and a positive definite (2,2)-block. Moreover, by similar theoretical analysis, we analyze the convergence conditions of the corresponding matrix splitting iteration methods and preconditioning properties of the MDSS preconditioned saddle point matrices. In final, one example is provided to confirm the effectiveness.
-
Keywords:
- Modified double /
- shift-splitting /
- saddle point problem /
- convergence /
- preconditioner /
- eigenvalue
-
-
References
[1] M. Ardeshiry, H. S. Goughery and H. N. Pour, New modified shift-splitting preconditioners for non-symmetric saddle point problems, Arab. J. Math., 2020, 9, 245–257. doi: 10.1007/s40065-019-0256-6 [2] M. Arioli, I. S. Duff and P. P. M. de Rijk, On the augmented system approach to sparse least-squares problems, Numer. Math., 1989, 55, 667–684. doi: 10.1007/BF01389335 [3] Z. -Z. Bai, Several splittings for non-Hermitian linear systems, Science in China, Series A: Math., 2008, 51,1339–1348. doi: 10.1007/s11425-008-0106-z [4] Z. -Z. Bai, Optimal parameters in the HSS-like methods for saddle-point problems, Numer. Linear Algebra Appl., 2009, 16, 447–479. doi: 10.1002/nla.626 [5] Z. -Z. Bai, M. Benzi and F. Chen, Modified HSS iteration methods for a class of complex symmetric linear systems, Comput., 2010, 87(3–4), 93–111. doi: 10.1007/s00607-010-0077-0 [6] Z. -Z. Bai, G. H. Golub and C. -K. Li, Convergence properties of preconditioned Hermitian and skew-Hermitian splitting methods for non-Hermitian positive semidefinite matrices, Math. Comput., 2007, 76, 287–298. doi: 10.1090/S0025-5718-06-01892-8 [7] Z. -Z. Bai, G. H. Golub and C. -K. Li, Optimal parameter in Hermitian and skew-Hermitian splitting method for certain twoby-two block matrices, SIAM J. Sci. Comput., 2006, 28, 583–603. doi: 10.1137/050623644 [8] Z. -Z. Bai, G. H. Golub, L. -Z. Lu and J. -F. Yin, Block-Triangular and skew-Hermitian splitting methods for positive definite linear systems, SIAM J. Sci. Comput., 2005, 26, 844–863. doi: 10.1137/S1064827503428114 [9] Z. -Z. Bai, G. H. Golub and K. N. Michael, On inexact hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems, Linear Algebra Appl., 2008, 428, 413–440. doi: 10.1016/j.laa.2007.02.018 [10] Z. -Z. Bai, G. H. Golub and M. K. Ng, Hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems, SIAM J. Matrix. Anal. A, 2003, 24, 603–626. doi: 10.1137/S0895479801395458 [11] Z. -Z. Bai, G. H. Golub and M. K. Ng, On successive-overrelaxation acceleration of the Hermitian and skew-Hermitian splitting iterations, Numer. Linear Algebra Appl., 2007, 14, 319–335. doi: 10.1002/nla.517 [12] Z. -Z. Bai, G. H. Golub and J. -Y. Pan, Preconditioned Hermitian and Skew-Hermitian Splitting Methods for Non-Hermitian Positive Semidefinite Linear Systems. Technical Report SCCM-02-12, Scientific Computing and Computational Mathematics Program, Department of Computer Science, Stanford University, Stanford, CA, 2002. [13] Z. -Z. Bai, G. H. Golub and J. -Y. Pan, Preconditioned Hermitian and skew-Hermitian splitting methods for non-Hermitian positive semidefinite linear systems, Numer. Math., 2004, 98, 1–32. doi: 10.1007/s00211-004-0521-1 [14] Z. -Z. Bai and M. K. Ng, On inexact preconditioners for nonsymmetric matrices, SIAM J. Sci. Comput., 2005, 26, 1710–1724. doi: 10.1137/040604091 [15] Z. -Z. Bai, M. K. Ng and Z. -Q. Wang, Constraint preconditioners for symmetric indefinite matrices, SIAM J. Matrix Anal. Appl., 2009, 31, 410–433. doi: 10.1137/080720243 [16] Z. -Z. Bai, B. N. Parlett and Z. Q. Wang, On generalized successive overrelaxation methods for augmented linear systems, Numer. Math., 2005, 102, 1–38. doi: 10.1007/s00211-005-0643-0 [17] Z. -Z. Bai and Z. -Q. Wang, On parameterized inexact Uzawa methods for generalized saddle point problems, Linear Algebra Appl., 2008, 428, 2900–2932. doi: 10.1016/j.laa.2008.01.018 [18] Z. -Z. Bai and X. Yang, On HSS-based iteration methods for weakly nonlinear systems, Appl. Numer. Math., 2009, 59, 2923–2936. doi: 10.1016/j.apnum.2009.06.005 [19] Z. -Z. Bai, J. -F. Yin and Y. -F. Su, A shift-splitting preconditioner for non-Hermitian positive definite matrices, J. Comput. Math., 2006, 24, 539–552. [20] Y. Cao, A general class of shift-splitting preconditioners for non-Hermitian saddle point problems with applications to time-harmonic eddy current models, Comput. Math. Appl., 2018, 77(4), 1124–1143. [21] Y. Cao, J. Du and Q. Niu, Shift-splitting preconditioners for saddle point problems, J. Comput. Appl. Math., 2014, 272,239–250. doi: 10.1016/j.cam.2014.05.017 [22] Y. Cao, L. -Q. Yao and M. -Q. Jiang, A modified dimensional split preconditioner for generalized saddle point problems, J. Comput. Appl. Math., 2013, 250, 70–82. doi: 10.1016/j.cam.2013.02.017 [23] Y. Cao, L. -Q. Yao, M. -Q. Jiang and Q. Niu, A relaxed HSS preconditioner for saddle point problems from meshfree discretization, J. Comput. Math., 2013, 31, 398–421. doi: 10.4208/jcm.1304-m4209 [24] C. -R. Chen and C. -F. Ma, A generalized shift-splitting preconditioner for saddle point problems, Appl. Math. Lett., 2015, 43, 49–55. doi: 10.1016/j.aml.2014.12.001 [25] F. Chen and Y. -L. Jiang, A generalization of the inexact parameterized Uzawa methods for saddle point problems, Appl. Math. Comput., 2008, 206, 765–771. [26] D. S. Daniela and D. Orban, Constraint-preconditioned Krylov solvers for regularized saddle-point systems, SIAM J. Sci. Comput., 2021, 43(2), A1001–A1026. doi: 10.1137/19M1291753 [27] M. T. Darvishi and P. Hessari, Symmetric SOR method for augmented systems, Appl. Math. Comput., 2006, 183, 409–415. [28] H. Elman and G. H. Golub, Inexact and preconditioned Uzawa algorithms for saddle point problems, SIAM J. Numer. Anal., 1994, 31,1645–1661. doi: 10.1137/0731085 [29] H. Elman and D. Silvester, Fast nonsymmetric iterations and preconditioning for Navier-Stokes equations, SIAM J. Sci. Comput., 1996, 17, 33–46. doi: 10.1137/0917004 [30] H. T. Fan, X. Y. Zhu and B. Zheng, The generalized double shift-splitting preconditioner for nonsymmetric generalized saddle point problems from the steady Navier-Stokes equations, Comp. Appl. Math., 2018, 37(3), 3256–3266. doi: 10.1007/s40314-017-0510-5 [31] B. Fischer, A. Ramage, D. J. Silvester and A. J. Wathen, Minimum residual methods for augmented systems, BIT, 1998, 38, 527–543. doi: 10.1007/BF02510258 [32] G. H. Golub, X. Wu and J. -Y. Yuan, SOR-like methods for augmented systems, BIT, 2001, 55, 71–85. [33] M. -Q. Jiang and Y. Cao, On local Hermitian skew-Hermitian splitting iteration methods for generalized saddle point problems, J. Comput. Appl. Math., 2009, 231, 973–982. doi: 10.1016/j.cam.2009.05.012 [34] Y. Liang, H. Xiang and S. Zhang, Preconditioners and their analyses for edge element saddle-point systems arising from time-harmonic Maxwell's equations, Numer. Algor., 2021, 86, 281–302. doi: 10.1007/s11075-020-00889-7 [35] X. -F. Peng and W. Li, On unsymmetric block overrelaxation-type methods for saddle point, Appl. Math. Comput, 2008, 203(2), 660–671. [36] D. K. Salkuyeh, M. Masoudi and D. Hezari, On the generalized shift-splitting preconditioner for saddle point problems, Appl. Mathe. Lett., 2015, 48, 55–61. doi: 10.1016/j.aml.2015.02.026 [37] C. H. Santos, B. P. B. Silva and J. -Y. Yuan, Block SOR methods for rank deficient least squares problems, J. Comput. Appl. Math., 1998, 100, 1–9. doi: 10.1016/S0377-0427(98)00114-9 [38] C. F. Théophile and P. Vega, Frequency-explicit a posteriori error estimates for finite element discretizations of Maxwell's equations, SIAM J. Numer. Anal., 2022, 60(4), 1774–1798. doi: 10.1137/21M1421805 [39] H. A. Van der Vorst, Iterative Krylov Methods for Large Linear Systems, Cambridge Monographs on Applied and Computational Mathematics, Cambridge University Press, Cambridge, UK, 2003. [40] L. Wang and Z. -Z. Bai, Convergence conditions for splitting iteration methods for non-Hermitian linear systems, Linear Algebra Appl., 2008, 428, 453–468. doi: 10.1016/j.laa.2007.03.001 [41] T. Wei and L. -T. Zhang, A new generalized shift-splitting method for nonsymmetric saddle point problems, Adv. Mech. Eng., 2022, 14(8), 1–11. [42] S. Wright, Stability of augmented system factorizations in interior-point methods, SIAM J. Matrix Anal. Appl., 1997, 18, 191–222. doi: 10.1137/S0895479894271093 [43] S. -L. Wu, T. -Z. Huang and X. -L. Zhao, A modified SSOR iterative method for augmented systems, J. Comput. Appl. Math., 2009, 228(1), 424–433. doi: 10.1016/j.cam.2008.10.006 [44] S. -L. Wu and D. K. Salkuyeh, A shift-splitting preconditioner for asymmetric saddle point problems, Comp. Appl. Math., 2020, 39(4), 314. doi: 10.1007/s40314-020-01364-8 [45] D. M. Young, Iteratin Solution for Large Systems, Academic Press, New York, 1971. [46] J. -Y. Yuan, Numerical methods for generalized least squares problems, J. Comput. Appl. Math., 1996, 66, 571–584. doi: 10.1016/0377-0427(95)00167-0 [47] J. -Y. Yuan and A. N. Iusem, Preconditioned conjugate gradient method for generalized least squares problems, J. Comput. Appl. Math., 1996, 71, 287–297. doi: 10.1016/0377-0427(95)00239-1 [48] G. -F. Zhang and Q. -H. Lu, On generalized symmetric SOR method for augmented systems, J. Comput. Appl. Math., 2008, 1(15), 51–58. [49] L. -T. Zhang, A new preconditioner for generalized saddle matrices with highly singular(1,1) blocks, Int. J. Comput. Math., 2014, 91(9), 2091–2101. doi: 10.1080/00207160.2013.867953 [50] L. -T. Zhang, A parameterized shift-splitting preconditioner for saddle point problems, Math. Biosci. Eng., 2019, 16(2), 1021–1033. doi: 10.3934/mbe.2019048 [51] L. -T. Zhang, Convergence of Newton-relaxed non-stationary multisplitting multi-parameters methods for nonlinear equations, J. Internet Technol., 2019, 20(3), 817–826. [52] L. -T. Zhang, T. Huang, S. Cheng and T. Gu, The weaker convergence of non-stationary matrix multisplitting methods for almost linear systems, Taiwan. J. Math., 2011,15(4), 1423–1436. [53] L. -T. Zhang, T. -Z. Huang, S. -H. Cheng and Y. -P. Wang, Convergence of a generalized MSSOR method for augmented systems, J. Comput. Appl. Math., 2012,236, 1841–1850. [54] L. -T. Zhang, D. -D. Jiang, X. -Y. Zuo and Y. -C. Zhao, Weaker convergence of global relaxed multisplitting USAOR methods for an H-matrix, Mob. Netw. Appl., 2021, 26, 755–765. [55] L. -T. Zhang and L. -M. Shi, An improved generalized parameterized inexact uzawa method for singular saddle point problems, J. Comput. Anal. Appl., 2017, 23(4), 671–683. [56] L. -T. Zhang and Y. -F. Zhang, A modified variant of HSS preconditioner for generalized saddle point problems, Adv. Mech. Eng., 2022, 14(7), 1–15. [57] L. -T. Zhang, Y. -F. Zhang, X. -J. Zhang and J. -F. Zhao, A accelerated modified shift-splitting method for nonsymmetric saddle problems, J. Appl. Anal. Comput., 2023, 13(4), 2283–2296. [58] L. -T. Zhang, X. -J. Zhang and J. -F. Zhao, A parameter shift-splitting iterative method for complex symmetric linear systems, J. Appl. Anal. Comput., 2024, 14(5), 2877–2889. [59] L. -T. Zhang, Y. -C. Zhao, Y. -F. Zhang and H. -K. Li, Relaxed modulus-based synchronous multisplitting multi-parameter methods for linear complementarity problems, J. Appl. Anal. Comput., 2021, 26, 745–754. [60] B. Zheng, Z. -Z. Bai and X. Yang, On semi-convergence of parameterized Uzawa methods for singular saddle point problems, Linear Algebra Appl., 2009, 431, 808–817. [61] S. -W. Zhou, A. -L. Yang, Y. Dou and Y. -J. Wu, The modified shift-splitting preconditioners for nonsymmetric saddle-point problems, Appl. Math. Lett., 2016, 59, 109–114. -
-
Figures(7) / Tables(4)
Export File
Citation
Litao Zhang, Haochen Zhao, Guangxu Zhu, Xiaojing Zhang. THE MODIFIED DOUBLE SHIFT-SPLITTING PRECONDITIONER FOR NONSYMMETRIC GENERALIZED SADDLE POINT PROBLEMS FROM THE TIME-HARMONIC MAXWELL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1520-1535. doi: 10.11948/20240279
Format
Content
DownLoad:
-
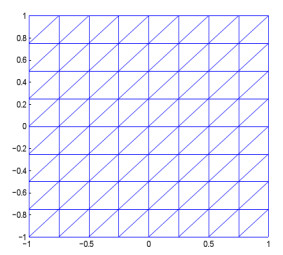
Figure 1.
A uniform mesh with
$ h=\frac{\sqrt{2}}{4} $ -
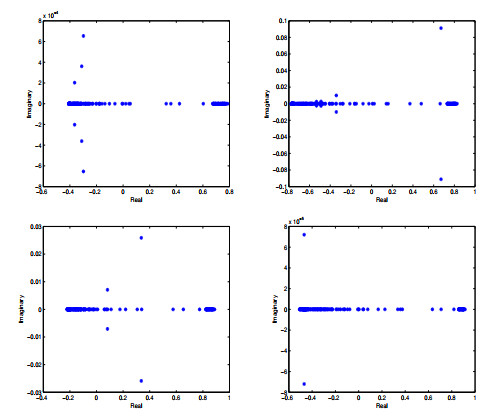
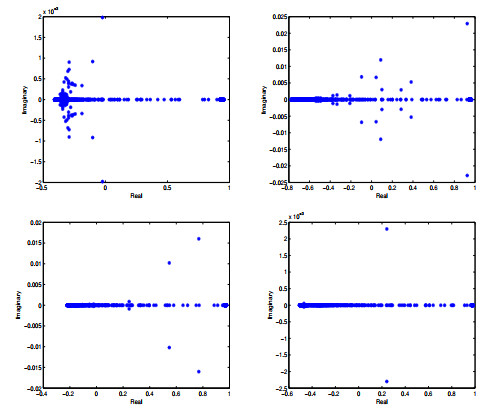
Figure 2.
The eigenvalue distribution for the MDSS iteration matrix
$ \Gamma=\mathcal {P}_{MDSS}^{-1}\mathcal {R}_{MDSS} $ $ \alpha=0.3, \beta=0.4, \gamma=1.4 $ $ \alpha=0.4, \beta=0.8, \gamma=1.1 $ $ \alpha=0.6, \beta=0.4, \gamma=1.6 $ $ \alpha=0.8, \beta=0.2, \gamma=1.3 $ $ h=\frac{\sqrt{2}}{8}. $ -
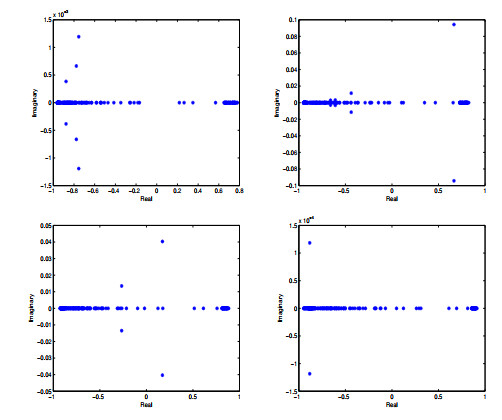
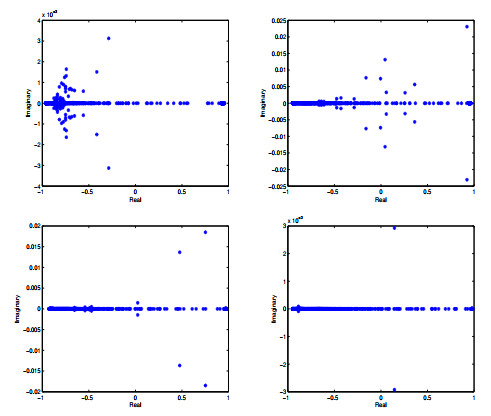
Figure 3.
The eigenvalue distribution for the GDSS iteration matrix
$ \Gamma=\mathcal {P}_{GDSS}^{-1}\mathcal {R}_{GDSS} $ $ \alpha=0.3, \beta=0.4 $ $ \alpha=0.4, \beta=0.8 $ $ \alpha=0.6, \beta=0.4 $ $ \alpha=0.8, \beta=0.2 $ $ h=\frac{\sqrt{2}}{8}. $ -
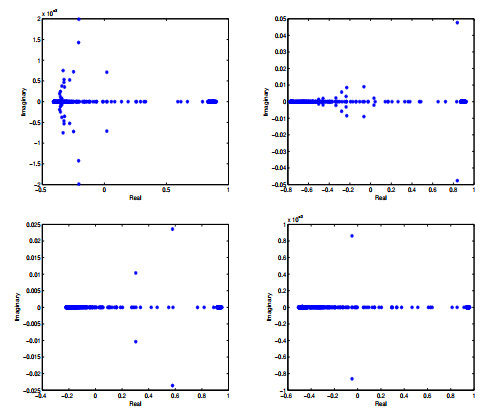
Figure 4.
The eigenvalue distribution for the MDSS iteration matrix
$ \Gamma=\mathcal {P}_{MDSS}^{-1}\mathcal {R}_{MDSS} $ $ \alpha=0.3, \beta=0.4, \gamma=1.4 $ $ \alpha=0.4, \beta=0.8, \gamma=1.1 $ $ \alpha=0.6, \beta=0.4, \gamma=1.6 $ $ \alpha=0.8, \beta=0.2, \gamma=1.3 $ $ h=\frac{\sqrt{2}}{12}. $ -
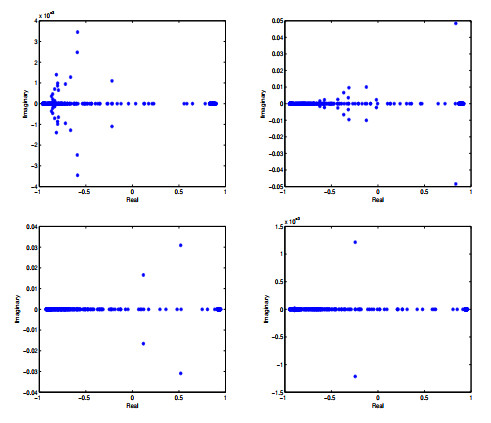
Figure 5.
The eigenvalue distribution for the GDSS iteration matrix
$ \Gamma=\mathcal {P}_{GDSS}^{-1}\mathcal {R}_{GDSS} $ $ \alpha=0.3, \beta=0.4 $ $ \alpha=0.4, \beta=0.8 $ $ \alpha=0.6, \beta=0.4 $ $ \alpha=0.8, \beta=0.2 $ $ h=\frac{\sqrt{2}}{12}. $ -
Figure 6.
The eigenvalue distribution for the MDSS iteration matrix
$ \Gamma=\mathcal {P}_{MDSS}^{-1}\mathcal {R}_{MDSS} $ $ \alpha=0.3, \beta=0.4, \gamma=1.4 $ $ \alpha=0.4, \beta=0.8, \gamma=1.1 $ $ \alpha=0.6, \beta=0.4, \gamma=1.6 $ $ \alpha=0.8, \beta=0.2, \gamma=1.3 $ $ h=\frac{\sqrt{2}}{18}. $ -
Figure 7.
The eigenvalue distribution for the GDSS iteration matrix
$ \Gamma=\mathcal {P}_{GDSS}^{-1}\mathcal {R}_{GDSS} $ $ \alpha=0.3, \beta=0.4 $ $ \alpha=0.4, \beta=0.8 $ $ \alpha=0.6, \beta=0.4 $ $ \alpha=0.8, \beta=0.2 $ $ h=\frac{\sqrt{2}}{18}. $