| Citation: |
Yi Gong. A HERMITE FINITE ELEMENT METHOD FOR THE VIBRATION PROBLEM OF THE RAYLEIGH-BISHOP BEAM[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 1134-1145. doi: 10.11948/20240285
|
A HERMITE FINITE ELEMENT METHOD FOR THE VIBRATION PROBLEM OF THE RAYLEIGH-BISHOP BEAM
-
Abstract
In this paper, a Hermite finite element method is proposed for the Rayleigh-Bishop equation which describes the vibration problem of the Rayleigh-Bishop beam. We first present the semi-discrete Galerkin finite element form for the Rayleigh-Bishop equation. Then by means of the cubic Hermite element, a full-discrete finite element scheme is established. Furthermore, a numerical algorithm based on the Hermite finite element method is proposed to solve the fourth-order Rayleigh-Bishop equation. Finally, a numerical example is given to illustrate the effectiveness of the proposed method. The Hermite finite element method is potentially applied to other vibration problems.
-
-
References
[1] L. N. Bondar and G. V. Demidenko, Solvability of the Cauchy problem for a pseudohyperbolic system, Complex Variables and Elliptic Equations, 2021, 66, 1084–1099. doi: 10.1080/17476933.2020.1829606 [2] E. Carrera and D. Scano, Finite elements based on Jacobi shape functions for the free vibration analysis of beams, plates, and shells, Mechanics of Advanced Materials and Structures, 2024, 31, 4–12. doi: 10.1080/15376494.2023.2219438 [3] C. Chazal and R. M. Pitti, Integral approach for time dependent materials using finite element method, Journal of Theoretical and Applied Mechanics, 2011, 49, 1029–1048. [4] Z. Chen, Z. Yang, N. Guo and G. Zhang, An energy finite element method for high frequency vibration analysis of beams with axial force, Applied Mathematical Modelling, 2018, 61, 521–539. doi: 10.1016/j.apm.2018.04.016 [5] A. Dabbagh, A. Rastgoo and F. Ebrahimi, Finite element vibration analysis of multi-scale hybrid nanocomposite beams via a refined beam theory, Thin-Walled Structures, 2019, 140, 304–317. doi: 10.1016/j.tws.2019.03.031 [6] B. Deka, P. Roy and N. Kumar, Weak Galerkin finite element methods combined with Crank-Nicolson scheme for parabolic interface problems, Journal of Applied Analysis and Computation, 2020, 10, 1433–1442. [7] G. V. Demidenko, Solvability conditions of the Cauchy problem for pseudohyperbolic equations, Siberian Mathematical Journal, 2015, 56, 1028–1041. doi: 10.1134/S0037446615060075 [8] G. V. Demidenko and S. V. Upsenskii, Partial differential equations and systems not solvable with respect to the highest-order derivative, New York, Marcel Dekker, 2003. [9] H. Elhuni and D. Basu, Dynamic soil structure interaction model for beams on viscoelastic foundations subjected to oscillatory and moving loads, Computers and Geotechnics, 2019, 115, 103157. doi: 10.1016/j.compgeo.2019.103157 [10] I. A. Fedotov, A. D. Polyanin, M. Y. Shatalov and H. M. Tenkam, Longitudinal vibrations of a Rayleigh-Bishop rod, Doklady Physics, 2010, 55, 609–614. doi: 10.1134/S1028335810120062 [11] A. C. Galucio, J. F. Deü and R. Ohayon, Finite element formulation of viscoelastic sandwich beams using fractional derivative operators, Computational Mechanics, 2004, 33, 282–291. doi: 10.1007/s00466-003-0529-x [12] H. Guo, X. Cao, Z. Liang, S. Lin, H. Zheng and H. Cui, Hermitian numerical manifold method for large deflection of irregular Föppl-von Kármán plates, Engineering Analysis with Boundary Elements, 2023, 153, 25–38. doi: 10.1016/j.enganabound.2023.05.008 [13] H. Guo, S. Lin and H. Zheng, GMLS-based numerical manifold method in mechanical analysis of thin plates with complicated shape or cutouts, Engineering Analysis with Boundary Elements, 2023, 151, 597–623. doi: 10.1016/j.enganabound.2023.03.028 [14] H. Guo and H. Rui, Least-squares Galerkin procedures for pseudohyperbolic equations, Applied Mathematics and Computation, 2007, 189, 425–439. doi: 10.1016/j.amc.2006.11.094 [15] F. Igor, S. Michael and M. Julian, Hyperbolic and pseudo-hyperbolic equations in the theory of vibration, Acta Mechanica, 2016, 227, 3315–3324. doi: 10.1007/s00707-015-1537-6 [16] K. Koutoati, F. Mohri and E. Carrera, A finite element approach for the static and vibration analyses of functionally graded material viscoelastic sandwich beams with nonlinear material behavior, Composite Structures, 2021, 274, 114315. doi: 10.1016/j.compstruct.2021.114315 [17] H. Liu and P. Huang, A two-grid decoupled finite element method for the stationary closed-loop geothermal system, Journal of Applied Analysis and Computation, 2023, 13, 1837–1851. [18] Y. Liu and H. Li, H1-Galerkin mixed finite element methods for pseudo-hyperbolic equations, Applied Mathematics and Computation, 2009, 212, 446–457. doi: 10.1016/j.amc.2009.02.039 [19] J. Marais, I. Fedotov and M. Shatalov, Longitudinal vibrations of a cylindrical rod based on the Rayleigh-Bishop theory, Afrika Matematika, 2015, 26, 1549–1560. doi: 10.1007/s13370-014-0286-3 [20] J. Niiranen, V. Balobanov, J. Kiendl and S. Hosseini, Variational formulations, model comparisons and numerical methods for Euler-Bernoulli micro-and nano-beam models, Mathematics and Mechanics of Solids, 2019, 24, 312–335. doi: 10.1177/1081286517739669 [21] F. P. Pinnola, M. S. Vaccaro, R. Barretta and F. M. de Sciarra, Finite element method for stress-driven nonlocal beams, Engineering Analysis with Boundary Elements, 2022, 134, 22–34. doi: 10.1016/j.enganabound.2021.09.009 [22] E. D. Sánchez, L. G. Nallim, F. J. Bellomo and S. H. Oller, Generalized viscoelastic model for laminated beams using hierarchical finite elements, Composite Structures, 2022, 235, 111794. [23] M. Shatalov, J. Marais, I. Fedotov, M. D. Tenkam and M. Schmidt, Longitudinal vibration of isotropic solid rods: From classical to modern theories, Advances in Computer Science and Engineering, 2011, 212, 187–214. [24] S. R. Singiresu, Vibration of Continuous Systems, Hoboken, NJ, USA, John Wiley & Sons, 2019. [25] Y. Tang and Z. Yin, Hermite finite element method for a class of viscoelastic beam vibration problem, Engineering, 2021, 13, 463–471. doi: 10.4236/eng.2021.138033 [26] R. L. Taylor, F. C. Filippou, A. Saritas and F. Auricchio, A mixed finite element method for beam and frame problems, Computational Mechanics, 2003, 31, 192–203. doi: 10.1007/s00466-003-0410-y [27] Y. Wang, H. Ding and L. Q. Chen, Vibration of axially moving hyperelastic beam with finite deformation, Applied Mathematical Modelling, 2019, 71, 269–285. doi: 10.1016/j.apm.2019.02.011 [28] C. Yu, J. Zhang, Y. Chen, Y. Feng and A. Yang, A numerical method for solving fractional-order viscoelastic Euler-Bernoulli beams, Chaos, Solitons & Fractals, 2019, 128, 275–279. -
-
Figures(5) / Tables(2)
Export File
Citation
Yi Gong. A HERMITE FINITE ELEMENT METHOD FOR THE VIBRATION PROBLEM OF THE RAYLEIGH-BISHOP BEAM[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 1134-1145. doi: 10.11948/20240285
Format
Content
DownLoad:
-
Figure 1.
Schematic of a beam with fixed ends.
-
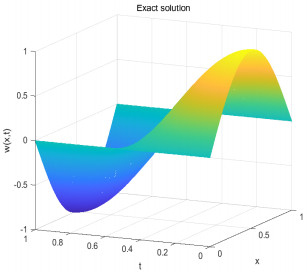
Figure 2.
The exact solution with
$ h=0.01 $ $ \tau=0.0001 $ -
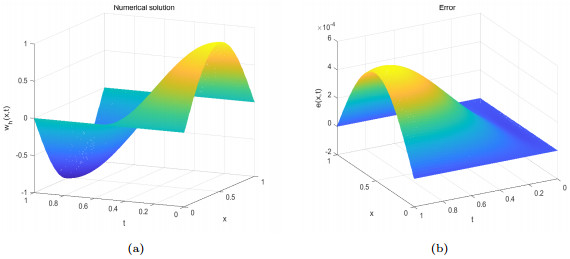
Figure 3.
The numerical solution and the error of the fully discrete scheme with
$ h=\frac{1}{10^2} $ $ \tau=\frac{1}{10^4} $ -
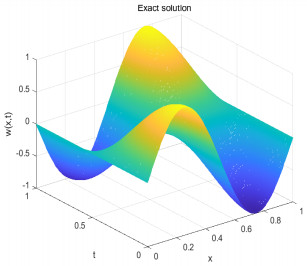
Figure 4.
The exact solution with
$ h=0.01 $ $ \tau=0.0001 $ -
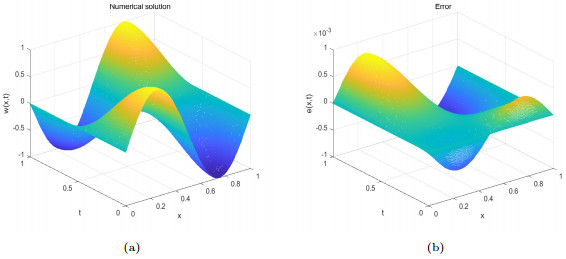
Figure 5.
The numerical solution and the error of the fully discrete scheme with
$ h=\frac{1}{10^2} $ $ \tau=\frac{1}{10^4} $