| Citation: | Ziqiang Wang, Xiao Wang, Junying Cao. HIGH-ORDER NUMERICAL SCHEME AND THEORETICAL ANALYSIS FOR NONLINEAR TWO-DIMENSIONAL FRACTIONAL VOLTERRA INTEGRAL EQUATIONS WITH INITIAL VALUE SINGULARITY[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3369-3402. doi: 10.11948/20240345 |
HIGH-ORDER NUMERICAL SCHEME AND THEORETICAL ANALYSIS FOR NONLINEAR TWO-DIMENSIONAL FRACTIONAL VOLTERRA INTEGRAL EQUATIONS WITH INITIAL VALUE SINGULARITY
-
Abstract
Various numerical methods have been proposed for solving one-dimensional weakly singular Volterra integral equations (VIEs) with smooth solutions. The main purpose of this paper is to propose and analyze a numerical method for the solution of two-dimensional nonlinear weakly singular VIEs with non-smooth solutions by involving the transformation of variables and modified Block-by-Block method. We rigorously prove that the new scheme can achieve an order of $ O(\tau_s^{3+\alpha}+\lambda_t^{3+\beta}) $ for non-smooth solutions with step size $ \tau_s,\lambda_t $ for $ 0<\alpha,\beta<1 $. Some numerical examples are conducted to support the theoretical results and demonstrate the effectiveness of the proposed method.
-

-
References
[1] H. Beyrami, T. Lotfi and K. Mahdiani, Stability and error analysis of the reproducing kernel Hilbert space method for the solution of weakly singular Volterra integral equation on graded mesh, Appl. Numer. Math., 2017, 120, 197–214. doi: 10.1016/j.apnum.2017.05.010 [2] J. Cao and C. Xu, A high order schema for the numerical solution of the fractional ordinary differential equations, J. Comput. Phys., 2013, 238, 154–168. doi: 10.1016/j.jcp.2012.12.013 [3] W. Cao, F. Zeng, Z. Zhang and G. E. Karniadakis, Implicit-explicit difference schemes for nonlinear fractional differential equations with nonsmooth solutions, SIAM J. Sci. Comput., 2016, 38, A3070–A3093. doi: 10.1137/16M1070323 [4] Y. Cao, T. Herdman and Y. Xu, A hybrid collocation method for Volterra integral equations with weakly singular kernels, SIAM J. Numer. Anal., 2003, 41, 364–381. doi: 10.1137/S0036142901385593 [5] Y. Chakir and H. Safouhi, Numerical solution of two-dimensional weakly singular Volterra integral equations of the first kind via bivariate rational approximants, J. Comput. Appl. Math., 2024, 436, 115378. DOI: 10.1016/j.cam.2023.115378. [6] Y. Chakir and H. Safouhi, On solving 2D weakly singular Volterra integral equations of the second kind, Numer. Algorithms, 2024. DOI: 10.1007/s11075-024-01854-4. [7] K. Diethelm, N. J. Ford and A. D. Freed, Detailed error analysis for a fractional Adams method, Numer. Algorithms, 2004, 36, 31–52. doi: 10.1023/B:NUMA.0000027736.85078.be [8] T. Diogo, P. Limam, A. Pedas and G. Vainikko, Smoothing transformation and spline collocation for weakly singular Volterra integro-differential equations, Appl. Numer. Math., 2017, 114, 63–76. doi: 10.1016/j.apnum.2016.08.009 [9] J. Dixon and S. McKee, Weakly singular discrete Gronwall inequalities, Z. Angew. Math. Mech., 1986, 66, 535–544. doi: 10.1002/zamm.19860661107 [10] C. Huang and M. Stynes, Spectral Galerkin methods for a weakly singular Volterra integral equation of the second kind, IMA J. Numer. Anal., 2017, 37, 1411–1436. [11] R. Katani and S. McKee, Numerical solution of two-dimensional weakly singular Volterra integral equations with non-smooth solutions, J. Comput. Appl. Math., 2022, 402, 113779. DOI: 10.1016/j.cam.2021.113779. [12] L. Li, D. Zhao, M. She and X. Chen, On high order numerical schemes for fractional differential equations by block-by-block approach, Appl. Math. Comput., 2022, 425, 127098. DOI: 10.1016/j.amc.2022.127098. [13] X. Li, T. Tang and C. Xu, Numerical solutions for weakly singular Volterra integral equations using Chebyshev and Legendre pseudo-spectral Galerkin methods, J. Sci. Comput., 2016, 67, 43–64. doi: 10.1007/s10915-015-0069-5 [14] X. Ma and C. Huang, Recovery of high order accuracy in spectral collocation method for linear Volterra integral equations of the third-kind with non-smooth solutions, J. Comput. Appl. Math., 2021, 392, 113458. DOI: 10.1016/j.cam.2021.113458. [15] Z. Ma, M. Stynes and C. Huang, Convergence and superconvergence of a fractional collocation method for weakly singular Volterra integro-differential equations, BIT, 2024, 64, 9. DOI: 10.1007/s10543-024-01011-2. [16] S. McKee, T. Tang and T. Diogo, An Euler-type method for two-dimensional Volterra integral equations of the first kind, IMA J. Numer. Anal., 2020, 20, 423–440. [17] M. Mostafazadeh and S. Shahmorad, Convergence analysis of Jacobi spectral tau-collocation method in solving a system of weakly singular Volterra integral equations, Math. Comput. Simulation, 2024, 223, 322–337. doi: 10.1016/j.matcom.2024.04.023 [18] M. Rasty and M. Hadizadeh, A product integration approach based on new orthogonal polynomials for nonlinear weakly singular integral equations, Acta Appl. Math., 2010, 109, 861–873. doi: 10.1007/s10440-008-9351-y [19] S. Arsalan Sajjadi, H. Saberi Najafi and H. Aminikhah, A numerical study on the non-smooth solutions of the nonlinear weakly singular fractional Volterra integro-differential equations, Math. Methods Appl. Sci., 2023, 46, 4070–4084. doi: 10.1002/mma.8741 [20] Y. Talaei, M. A. Zaky and A. S. Hendy, An easy-to-implement recursive fractional spectral-Galerkin method for multi-term weakly singular Volterra integral equations with non-smooth solutions, Numer. Algorithms, 2024. DOI: 10.1007/s11075-023-01742-3. [21] T. Wang, H. Lian and L. Ji, Singularity separation Chebyshev collocation method for weakly singular Volterra integral equations of the second kind, Numer. Algorithms, 2024, 95, 1829–1854. doi: 10.1007/s11075-023-01629-3 [22] Z. Wang, Q. Liu and J. Cao, A higher-order numerical scheme for two-dimensional nonlinear fractional Volterra integral equations with uniform accuracy, Fractal Fract., 2022, 6, 314. DOI: 10.3390/fractalfract6060314. [23] Z. Wang, Q. Tan, Z. Wang and J. Cao, Multiquadric quasi-interpolation method for fractional integral-differential equations, J. Appl. Anal. Comput., 2024, 14, 2534–2557. [24] G. Yao, Z. Wang and C. Zhang, A multi-domain hybrid spectral collocation method for nonlinear Volterra integral equations with weakly singular kernel, J. Comput. Appl. Math., 2024, 444, 115785. DOI: 10.1016/j.cam.2024.115785. [25] G. Zakeri and M. Navab, Sinc collocation approximation of non-smooth solution of a nonlinear weakly singular Volterra integral equation, J. Comput. Phys., 2010, 229, 6548–6557. doi: 10.1016/j.jcp.2010.05.010 [26] M. A. Zaky, Recovery of high order accuracy in Jacobi spectral collocation methods for fractional terminal value problems with non-smooth solutions, J. Comput. Appl. Math., 2019, 357, 103–122. doi: 10.1016/j.cam.2019.01.046 [27] M. A. Zaky, An accurate spectral collocation method for nonlinear systems of fractional differential equations and related integral equations with nonsmooth solutions, Appl. Numer. Math., 2020, 154, 205–222. doi: 10.1016/j.apnum.2020.04.002 -
-
-
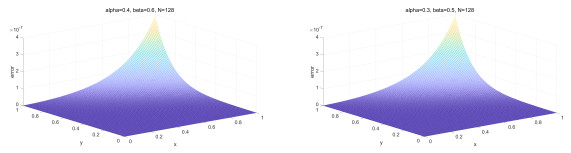
Figure 1.
Error distribution for
$ \alpha = 0.4, \beta = 0.6 $ $ \alpha = 0.3, \beta = 0.5 $ $ N = 128 $ -
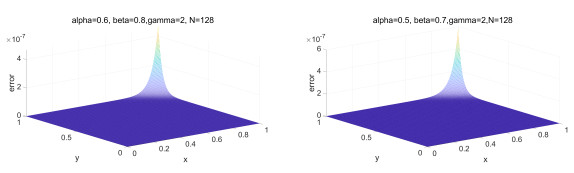
Figure 2.
Error distribution for
$ \alpha = 0.6, \beta = 0.8, \gamma = 4 $ $ \alpha = 0.2, \beta = 0.5 ,\gamma = 3 $ $ N = 128 $ -
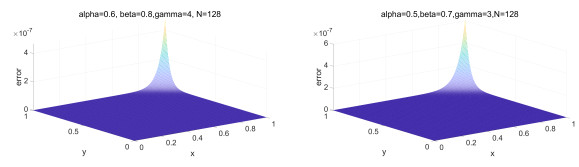
Figure 3.
Error distribution for
$ \alpha = 0.6, \beta = 0.8, \gamma = 4 $ $ \alpha = 0.5, \beta = 0.7, \gamma = 3 $ $ N = 128 $




 DownLoad:
DownLoad: