| Citation: |
Asma Rashid Butt, Zainab Rana, Dumitru Baleanu, Mustafa Bayram. EXPLORATION OF FRACTIONAL EFFECTS AND MULTI-STABILITY IN THE NONLINEAR (2+1)-DIMENSIONAL DAVEY-STEWARTSON FOKAS SYSTEM[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3345-3368. doi: 10.11948/20240518
|
EXPLORATION OF FRACTIONAL EFFECTS AND MULTI-STABILITY IN THE NONLINEAR (2+1)-DIMENSIONAL DAVEY-STEWARTSON FOKAS SYSTEM
-
Abstract
This work delves into a profound analysis of the fractional Davey-Stewartson Fokas system, which has applications in analyzing two-dimensional wave packets on water surfaces and modeling pulse propagation in optical fibers. An in-depth comparative study is conducted on the local M and the fractional beta derivatives to elucidate their effects on the system's solutions and to investigate the role of fractional parameters in shaping the system's behavior. Two approaches, the $ G'/(bG'+G+a) $ expansion and the Sardar sub-equation approaches, are employed to generate new solitary wave solutions that appear in the form of lump, periodic, singular, bright, and their combo solitons. The solutions are produced under constraint conditions and illustrated using 3D, density, and 2D plots by selecting appropriate values of parameters. Moreover, chaotic phenomena are analyzed through the observation of multi-stability by setting the parameters and varying initial conditions. The extracted solutions validate the effectiveness of the proposed methodologies in deriving exact solutions in nonlinear contexts.
-
-
References
[1] W. Albalawi, N. Raza, S. Arshed, M. Farman, K. S. Nisar and A. H. Abdel-Aty, Chaotic behavior and construction of a variety of wave structures related to a new form of generalized q-Deformed sinh-Gordon model using couple of integration norms, AIMS Mathematics, 2024, 9(4), 9536–9555. doi: 10.3934/math.2024466 [2] K. K. Ali, A. M. Wazwaz and M. S. Osman, Optical soliton solutions to the generalized nonautonomous nonlinear Schrödinger equations in optical fibers via the sine-Gordon expansion method, Optik, 2020, 208, 164132. doi: 10.1016/j.ijleo.2019.164132 [3] A. H. Arnous, A. R. Seadawy, R. T. Alqahtani and A. Biswas, Optical solitons with complex Ginzburg–Landau equation by modified simple equation method, Optik, 2017, 144, 475–480. doi: 10.1016/j.ijleo.2017.07.013 [4] D. Bahns, N. Pinamonti and K. Rejzner, Equilibrium states for the massive Sine-Gordon theory in the Lorentzian signature, Journal of Mathematical Analysis and Applications, 2023, 526(2), 127249. doi: 10.1016/j.jmaa.2023.127249 [5] H. M. Baskonus, New acoustic wave behaviors to the Davey–Stewartson equation with power-law nonlinearity arising in fluid dynamics, Nonlinear Dynamics, 2016, 86, 177–183. doi: 10.1007/s11071-016-2880-4 [6] A. R. Butt, N. Raza, M. Inc and R. T. Alqahtani, Complexitons, Bilinear forms and Bilinear Bäcklund transformation of a (2+1)-dimensional Boiti–Leon–Manna–Pempinelli model describing incompressible fluid, Chaos, Solitons and Fractals, 2023, 168, 113201. doi: 10.1016/j.chaos.2023.113201 [7] M. S. Ghayad, N. M. Badra, H. M. Ahmed and W. B. Rabie, Derivation of optical solitons and other solutions for nonlinear Schrödinger equation using modified extended direct algebraic method, Alexandria Engineering Journal, 2023, 64, 801–811. doi: 10.1016/j.aej.2022.10.054 [8] M. M. Hassan, Exact solitary wave solutions for a generalized KdV–Burgers equation, Chaos, Solitons and Fractals, 2004, 19(5), 1201–1206. doi: 10.1016/S0960-0779(03)00309-6 [9] B. Hong, Assorted exact explicit solutions for the generalized Atangana's fractional BBM–Burgers equation with the dissipative term, Frontiers in Physics, 2022, 10, 1071200. doi: 10.3389/fphy.2022.1071200 [10] A. J. M. Jawad, M. D. Petković and A. Biswas, Modified simple equation method for nonlinear evolution equations, Applied Mathematics and Computation, 2010, 217(2), 869–877. doi: 10.1016/j.amc.2010.06.030 [11] B. Kemaloğlu, G. Yel and H. Bulut, An application of the rational sine–Gordon method to the Hirota equation, Optical and Quantum Electronics, 2023, 55(7), 658. doi: 10.1007/s11082-023-04930-6 [12] S. Kumar, W. X. Ma, S. K. Dhiman and A. Chauhan, Lie group analysis with the optimal system, generalized invariant solutions, and an enormous variety of different wave profiles for the higher-dimensional modified dispersive water wave system of equations, The European Physical Journal Plus, 2023, 138(5), 434. doi: 10.1140/epjp/s13360-023-04053-7 [13] R. J. Kuo, M. R. Setiawan and T. P. Nguyen, Sequential clustering and classification using deep learning technique and multi-objective sine-cosine algorithm, Computers and Industrial Engineering, 2022, 173, 108695. doi: 10.1016/j.cie.2022.108695 [14] J. Lai, S. Mao, J. Qiu, H. Fan, Q. Zhang, Z. Hu and J. Chen, Investigation progresses and applications of fractional derivative model in geotechnical engineering, Mathematical Problems in Engineering, no. 1, 2016, 9183296. [15] L. F. Mollenauer and J. P. Gordon, Solitons in Optical Fibers: Fundamentals and Applications, Elsevier, 2006. [16] S. Momani and Z. Odibat, Analytical approach to linear fractional partial differential equations arising in fluid mechanics, Physics Letters A, 2006, 355(4–5), 271–279. [17] M. A. Murad, M. Iqbal, A. H. Arnous, A. Biswas, Y. Yildirim and A. S. Alshomrani, Optical dromions with fractional temporal evolution by enhanced modified tanh expansion approach, Journal of Optics, 2024, 1–10. [18] M. N. Rafiq, A. Majeed, S. W. Yao, M. Kamran, M. H. Rafiq and M. Inc, Analytical solutions of nonlinear time fractional evaluation equations via unified method with different derivatives and their comparison, Results in Physics, 2021, 26, 104357. doi: 10.1016/j.rinp.2021.104357 [19] R. U. Rahman, A. F. Al-Maaitah, M. Qousini, E. A. Az-Zobi, S. M. Eldin and M. Abuzar, New soliton solutions and modulation instability analysis of fractional Huxley equation, Results in Physics, 2023, 44, 106163. doi: 10.1016/j.rinp.2022.106163 [20] R. U. Rahman, M. M. Qousini, A. Alshehri, S. M. Eldin, K. El-Rashidy and M. S. Osman, Evaluation of the performance of fractional evolution equations based on fractional operators and sensitivity assessment, Results in Physics, 2023, 49, 106537. doi: 10.1016/j.rinp.2023.106537 [21] N. Raza, S. S. Kazmi and G. A. Basendwah, Dynamical analysis of solitonic, quasi-periodic, bifurcation and chaotic patterns of Landau–Ginzburg–Higgs model, Journal of Applied Analysis and Computation, 2024, 14(1), 197–213. doi: 10.11948/20230137 [22] N. Raza, M. H. Rafiq, M. Kaplan, S. Kumar and Y. M. Chu, The unified method for abundant soliton solutions of local time fractional nonlinear evolution equations, Results in Physics, 2021, 22, 103979. [23] H. Rezazadeh, S. M. Mirhosseini-Alizamini, A. Neirameh, A. Souleymanou, A. Korkmaz and A. Bekir, Fractional Sine–Gordon equation approach to the coupled higgs system defined in time-fractional form, Iranian Journal of Science and Technology, Transactions A: Science, 2019, 43, 2965–2973. [24] T. A. Sulaiman, A. Yusuf and A. Atangana, New lump, lump-kink, breather waves and other interaction solutions to the (3+1)-dimensional soliton equation, Communications in Theoretical Physics, 2020, 72(8), 085004. [25] K. L. Wang, New mathematical approaches to nonlinear coupled Davey– Stewartson Fokas system arising in optical fibers, Mathematical Methods in the Applied Sciences, 2024, (47), 12668–12683. [26] A. Yusuf, T. A. Sulaiman, M. Inc and M. Bayram, Breather wave, lump-periodic solutions and some other interaction phenomena to the Caudrey–Dodd–Gibbon equation, The European Physical Journal Plus, 2020, 135(7), 1–8. -
-
Figures(16)
Export File
Citation
Asma Rashid Butt, Zainab Rana, Dumitru Baleanu, Mustafa Bayram. EXPLORATION OF FRACTIONAL EFFECTS AND MULTI-STABILITY IN THE NONLINEAR (2+1)-DIMENSIONAL DAVEY-STEWARTSON FOKAS SYSTEM[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3345-3368. doi: 10.11948/20240518
Format
Content
DownLoad:
-
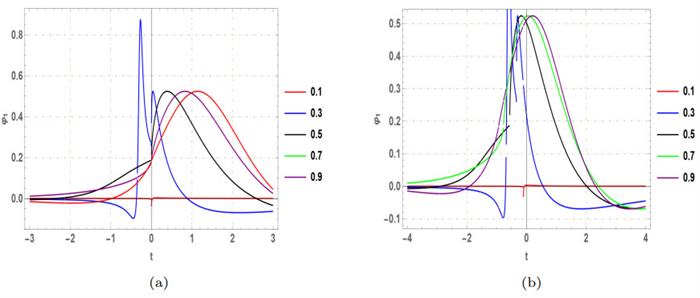
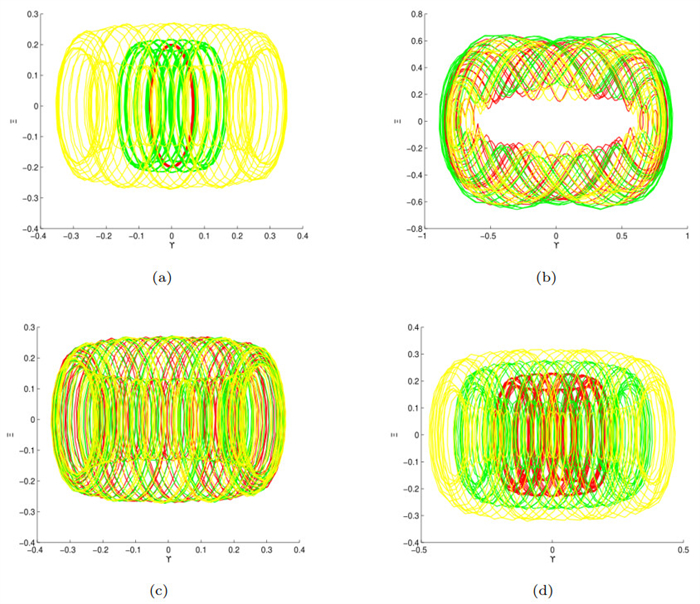
Figure 1.
Exploring chaotic tendencies via multi-stability investigation.
-
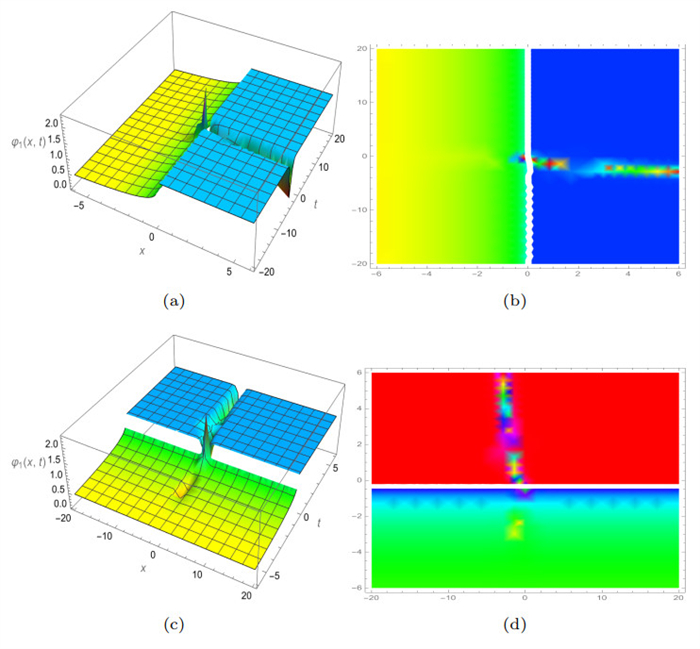
Figure 2.
3D and density plots of
$ Abs\left(\varphi_1 (x, y, t)\right) $ $ \gamma $ $ \beta=0.3 $ -
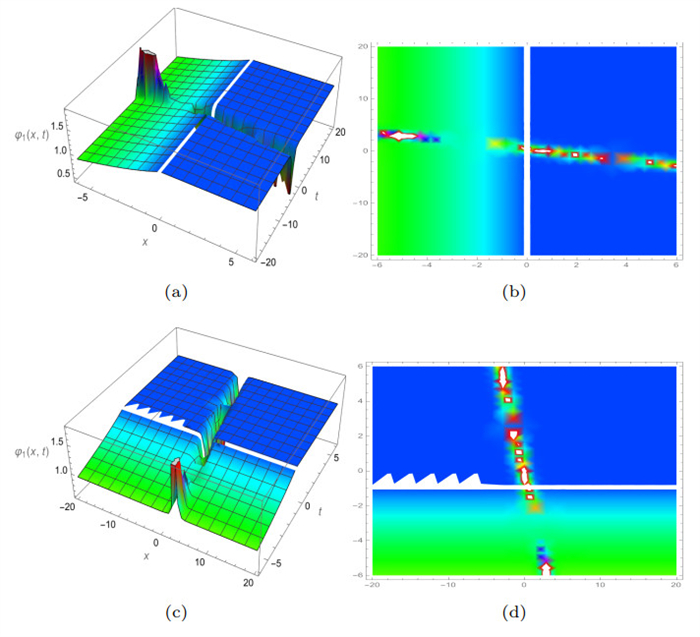
Figure 3.
3D and density plots of
$ Abs\left(\varphi_1 (x, y, t)\right) $ $ \gamma $ $ \beta=0.9 $ -
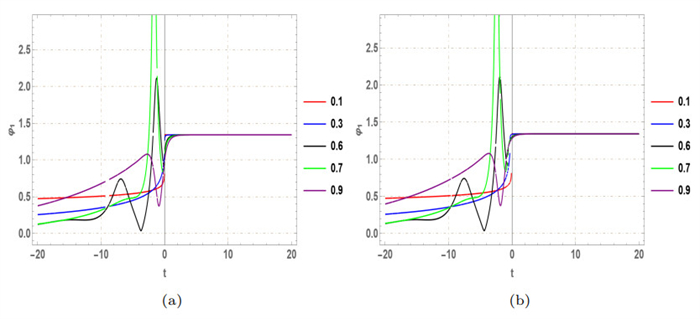
Figure 4.
2D delineation of
$ Abs\left(\varphi_1 (x, y, t)\right) $ $ \gamma $ $ \beta $ -
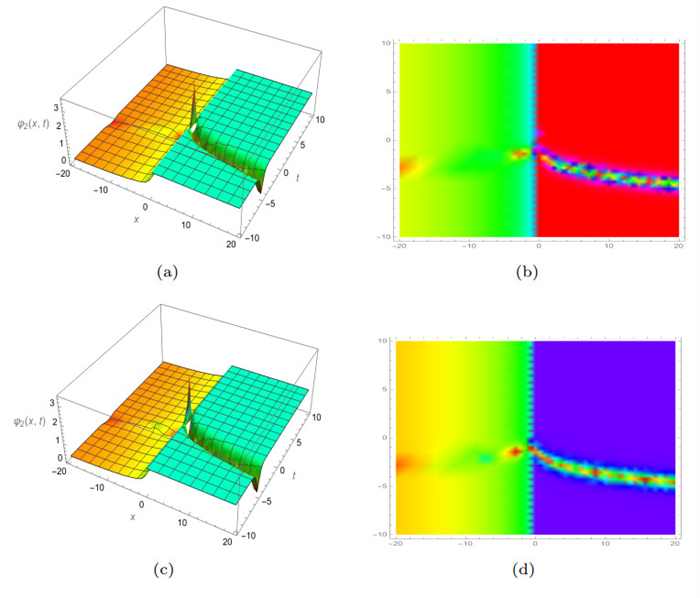
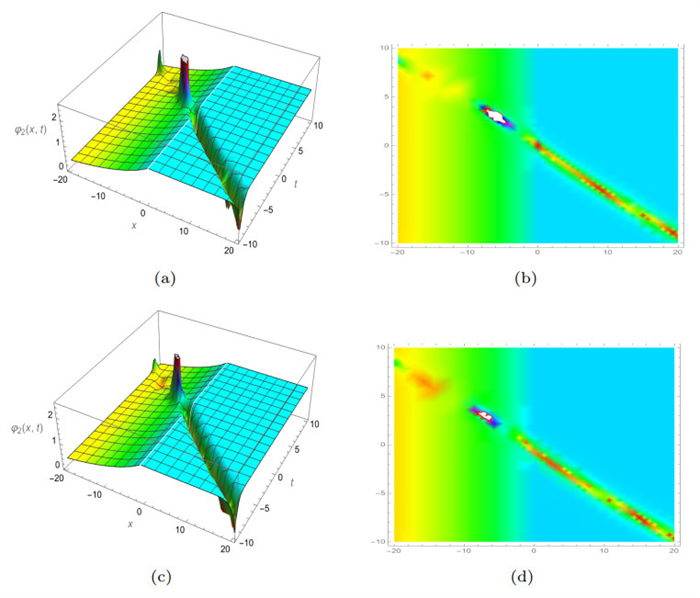
Figure 5.
3D and density plots of
$ Abs\left(\varphi_2 (x, y, t)\right) $ $ \gamma $ $ \beta=0.3 $ -
Figure 6.
3D and density plots of
$ Abs\left(\varphi_2 (x, y, t)\right) $ $ \gamma $ $ \beta=0.9 $ -
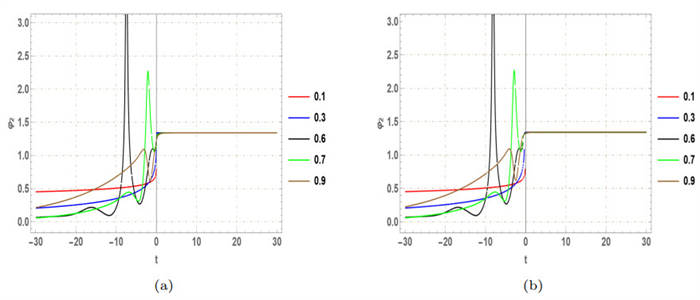
Figure 7.
2D depiction of
$ Abs\left(\varphi_2 (x, y, t)\right) $ $ \gamma $ $ \beta $ -
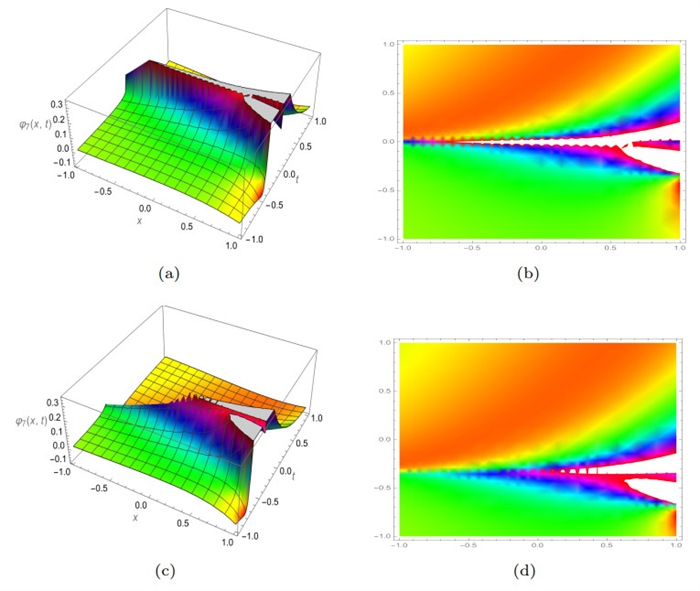
Figure 8.
3D and density plots of
$ Re\left(\varphi_7 (x, y, t)\right) $ $ \gamma $ $ \beta=0.3 $ -
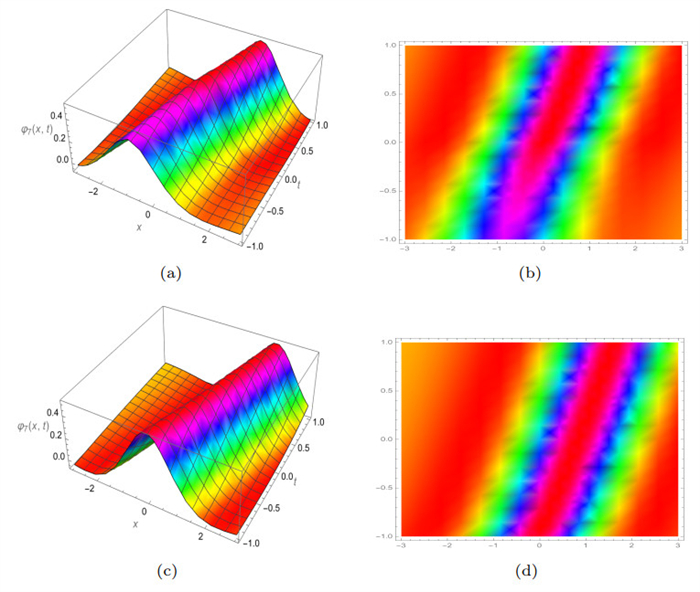
Figure 9.
3D and density plots of
$ Re\left(\varphi_7 (x, y, t)\right) $ $ \gamma $ $ \beta=0.9 $ -
Figure 10.
2D plots of
$ Abs\left(\varphi_7 (x, y, t)\right) $ $ \gamma $ $ \beta $ -
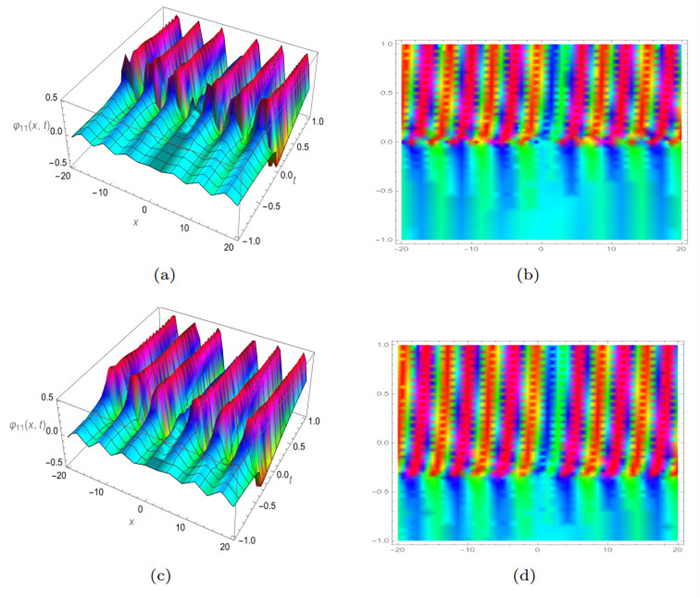
Figure 11.
3D and density plots of
$ Re\left(\varphi_{11} (x, y, t)\right) $ $ \gamma $ $ \beta=0.3 $ -
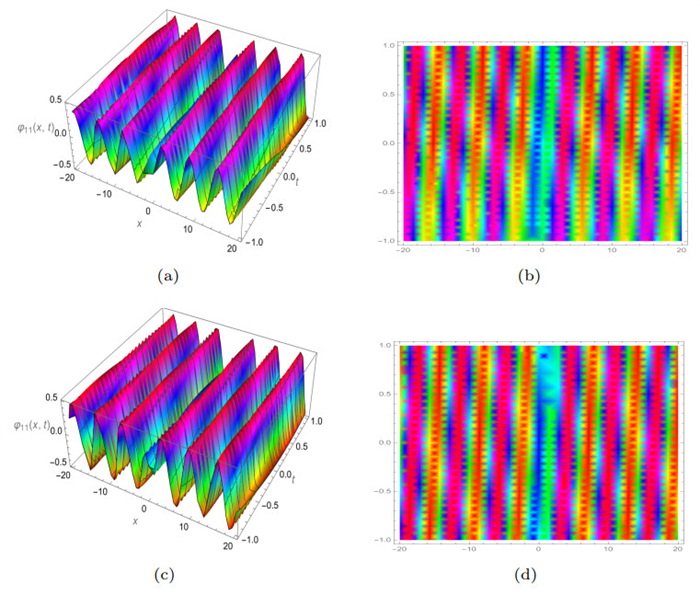
Figure 12.
3D and density plots of
$ Re\left(\varphi_{11} (x, y, t)\right) $ $ \gamma $ $ \beta=0.9 $ -
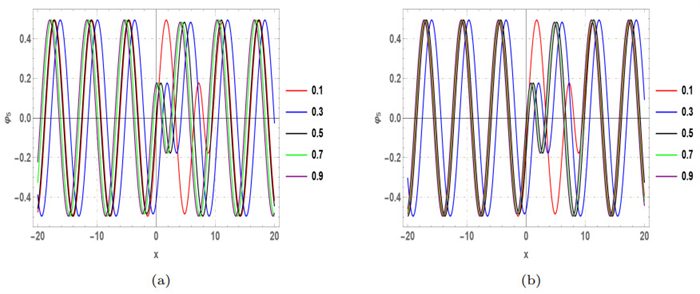
Figure 13.
2D delineation of
$ Abs\left(\varphi_{11} (x, y, t)\right) $ $ \gamma $ $ \beta $ -
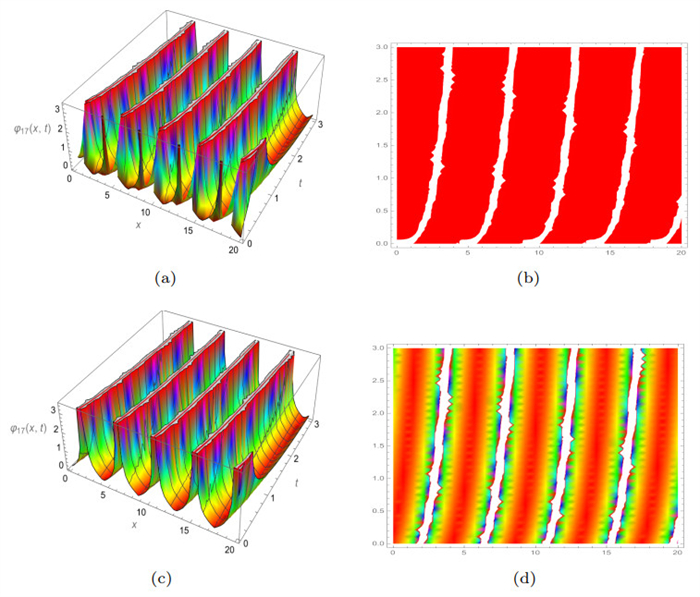
Figure 14.
3D and density plots of
$ Abs\left(\varphi_{17} (x, y, t)\right) $ $ \gamma $ $ \beta=0.3 $ -
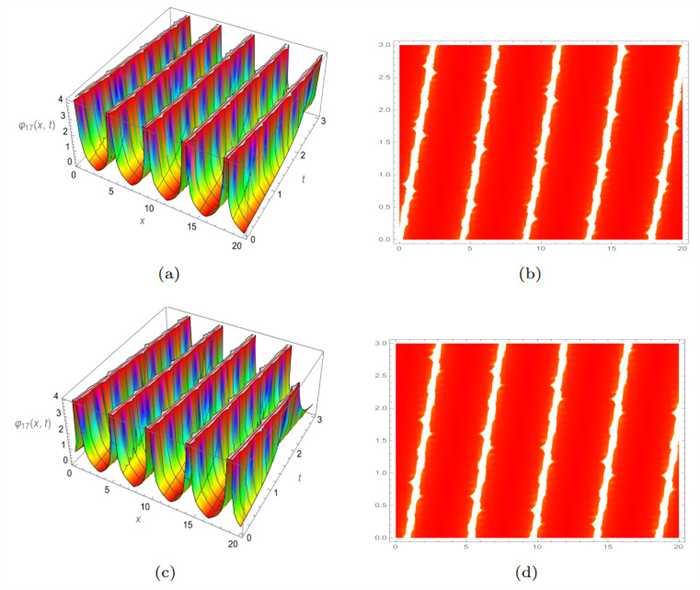
Figure 15.
3D and density plots of
$ Abs\left(\varphi_{17} (x, y, t)\right) $ $ \gamma $ $ \beta=0.9 $ -
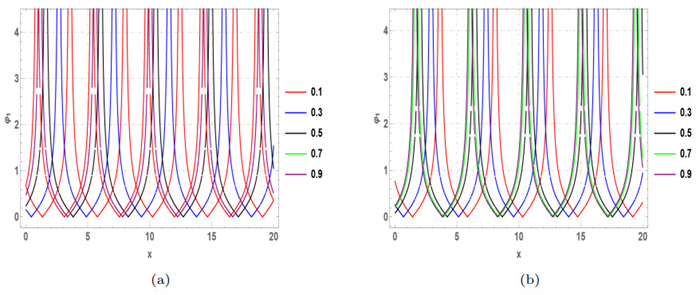
Figure 16.
2D depiction of
$ Abs\left(\varphi_{17} (x, y, t)\right) $ $ \gamma $ $ \beta $