| Citation: | Zhenping Li, Xiangtuan Xiong. A NEW ITERATION ALGORITHM WITH RELAXATION FACTOR FOR THE CAUCHY PROBLEM OF TIME-FRACTIONAL DIFFUSION EQUATION[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2959-2976. doi: 10.11948/20240354 |
A NEW ITERATION ALGORITHM WITH RELAXATION FACTOR FOR THE CAUCHY PROBLEM OF TIME-FRACTIONAL DIFFUSION EQUATION
-
Abstract
In this paper, we investigate a Cauchy problem for the time-fractional diffusion equation by using a new simplified iteration algorithm. The algorithm arises from the well-known Kozlov-Maz'ya iterative scheme for solving the Cauchy problem of classical ill-posed boundary value problems. A relaxation factor in the algorithm is introduced. Based on Fourier analysis, we give a choice rule for the relaxation factor. The iteration algorithm combined with a stopping criterion is given for stable numerical reconstruction of the solution. For illustration, several numerical experiments are constructed to demonstrate the feasibility and efficiency of the proposed method.
-

-
References
[1] E. E. Adams and L. W. Gelhar, Field-study of dispersion in a heterogeneous aquifer 2. spatial moment analysis, Water Resour. Res., 1992, 28(12), 3293–3307. doi: 10.1029/92WR01757 [2] S. Alimov and R. Ashurov, Inverse problem of determining an order of the Caputo time-fractional derivative for a subdiffusion equation, J. Inverse Ill-Posed Probl., 2020, 28(5), 651–658. doi: 10.1515/jiip-2020-0072 [3] E. Barkai, R. Metzler and J. Klafter, From continuous time random walks to the fractional Fokker-Planck equation, Phys. Rev. E, 2000, 61(1), 132–138. doi: 10.1103/PhysRevE.61.132 [4] G. Bastay, V. A. Kozlov and B. O. Turesson, Iterative methods for an inverse heat conduction problem, J. Inv. Ill-Posed Problems, 2001, 9(4), 375–388. doi: 10.1515/jiip.2001.9.4.375 [5] A. Blumen, G. Zumofen and J. Klafter, Transport aspects in anomalous diffusion: Lévy walks, Phys. Rev. A, 1989, 40, 3964–3973. doi: 10.1103/PhysRevA.40.3964 [6] A. N. Bondarenko and D. S. Ivaschenko, Numerical methods for solving inverse problems for time fractional diffusion equation with variable coefficient, J. Inv. Ill-Posed Problems, 2009, 17, 419–440. [7] J. P. Bouchaud and A. Georges, Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications, Phys. Rep., 1990, 195(4–5), 127–293. doi: 10.1016/0370-1573(90)90099-N [8] A. S. Chaves, A fractional diffusion equation to describe Lévy flights, Phys. Lett. A, 1998, 239, 13–16. doi: 10.1016/S0375-9601(97)00947-X [9] J. Cheng, J. Nakagawa, M. Yamamoto and T. Yamazaki, Uniqueness in an inverse problem for one-dimensional fractional diffusion equation, Inverse Probl., 2009, 25, 115002, 16 pp. doi: 10.1088/0266-5611/25/11/115002 [10] J. Cheng and M. Yamamoto, One new strategy for a priori choice of regularizing parameters in Tikhonov's regularization, Inverse Probl., 2000, 16, L31–L38. doi: 10.1088/0266-5611/16/4/101 [11] H. D. N. Duy, T. N. Huy, L. L. Dinh and G. Q. T. Le, Inverse problem for nonlinear backward space-fractional diffusion equation, J. Inverse Ill-Posed Probl., 2016, 25, 423–443. [12] H. W. Engl, M. Hanke and A. Neubauer, Regularization of Inverse Problems, Kluwer Academic Publisher, Dordrecht Boston London, 1996. [13] R. Gorenflo, F. Mainardi, D. Moretti, G. Pagnini and P. Paradisi, Discrete random walk models for space-time fractional diffusion, Chem. Phys., 2002, 284, 521–541. doi: 10.1016/S0301-0104(02)00714-0 [14] J. Hadamard, Lectures on Cauchy's Problem in Linear Partial Differential Equations, Dover Publications, New York, 1953. [15] Y. Hatano, N. Hatano, H. Amano, T. Ueno, A. K. Sukhoruchkin and S. V. Kazakov, Aerosol migration near Chernobyl: Long-term data and modeling, Atmos. Environ., 1998, 32, 2587–2594. doi: 10.1016/S1352-2310(97)00511-6 [16] Y. C. Hon and T. Wei, Backus-Gilbert algorithm for the Cauchy problem of the Laplace equation, Inverse Probl., 2001, 17, 261–271. doi: 10.1088/0266-5611/17/2/306 [17] Y. C. Hon and T. Wei, The method of fundamental solutions for solving multidimensional inverse heat conduction problems, Comp. Model. Eng. Sci., 2005, 7(2), 119–132. [18] S. Z. Jiang and T. Wei, Recovering a time-dependent potential function in a time fractional diffusion equation by using a nonlinear condition, Inverse Probl. Sc. En., 2021, 29(2), 174–195. doi: 10.1080/17415977.2020.1782399 [19] S. Z. Jiang and Y. J. Wu, Recovering a time-dependent potential function in a multi-term time fractional diffusion equation by using a nonlinear condition, J. Inverse Ill-Posed Probl., 2021, 29(2), 233–248. [20] M. Jourhmane and N. S. Mera, An iterative algorithm for the backward heat conduction problem based on variable relaxation factors, Inverse Problems in Engng, 2002, 10(4), 293–308. doi: 10.1080/10682760290004320 [21] A. B. Kostin and S. I. Piskarev, Inverse source problem for the abstract fractional differential equation, J. Inverse Ill-Posed Probl., 2021, 29(2), 267–281. doi: 10.1515/jiip-2020-0038 [22] V. A. Kozlov and V. G. Maz'ya, On iterative procedures for solving ill-posed boundary value problems that preserve differential equations, Leningrad Math. J., 1990, 1, 1207–1228. [23] L. Landweber, An iteration formula for Fredholm integral equations of the first kind, Am. J. Math., 1951, 73(3), 615–624. doi: 10.2307/2372313 [24] M. M. Meerschaert, D. A. Benson, H. P. Scheffer and B. Baeumer, Stochastic solution of space-time fractional diffusion equations, Phys. Rev. E, 2002, 65, 041103. [25] M. M. Meerschaert, J. Mortensen and S. W. Wheatcraft, Fractional vector calculus for fractional advection-dispersion, Phys. A, 2006, 367, 181–190. doi: 10.1016/j.physa.2005.11.015 [26] M. M. Meerschaert and H. P. Scheffer, Semistable Lévy Motion, Fract. Calc. Appl. Anal., 2002, 5(1), 27–54. [27] R. Metzler and J. Klafter, The random walk's guide to anomalous diffusion: A fractional dynamics approach, Phys. Rep., 2000, 339, 1–77. doi: 10.1016/S0370-1573(00)00070-3 [28] D. A. Murio, Stable numerical solution of a fractional-diffusion inverse heat conduction problem, Comput. Math. Appl., 2007, 53, 1492–1501. doi: 10.1016/j.camwa.2006.05.027 [29] D. A. Murio, Implicit finite difference approximation for time fractional diffusion equations, Comput. Math. Appl., 2008, 56, 1138–1145. doi: 10.1016/j.camwa.2008.02.015 [30] S. Nemati, P. M. Lima and S. Sedaghat, Legendre wavelet collocation method combined with the Gauss-Jacobi quadrature for solving fractional delay-type integro-differential equations, Appl. Numer. Math., 2020, 149, 99–112. doi: 10.1016/j.apnum.2019.05.024 [31] I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999. [32] M. Raberto, E. Scalas and F. Mainardi, Waiting-times and returns in high-frequency financial data: An empirical study, Phys. A, 2002, 314(1), 749–755. [33] L. Sabatelli, S. Keating, J. Dudley and P. Richmond, Waiting time distributions in financial markets, Eur. Phys. J. B, 2002, 27, 273–275. [34] H. Scher and E. W. Montroll, Anomalous transit-time dispersion in amorphous solids, Phys. Rev. B, 1975, 12(6), 2455–2477. [35] A. H. Salehi Shayegan and A. Zakeri, A numerical method for determining a quasi solution of a backward time-fractional diffusion equation, Inverse Probl. Sci. En., 2018, 26(8), 1130–1154. doi: 10.1080/17415977.2017.1384826 [36] I. M. Sokolov, J. Klafter and A. Blumen, Fractional kinetics, Phys. Today, 2002, 55(11), 48–54. doi: 10.1063/1.1535007 [37] T. L. Szabo and J. Wu, A model for longitudinal and shear wave propagation in viscoelastic media, J. Acoust. Soc. Am., 2000, 107(5), 2437–2446. [38] T. Wei, X. L. Li and Y. S. Li, An inverse time-dependent source problem for a time-fractional diffusion equation, Inverse Probl., 2016, 32(8), 085003. [39] X. T. Xiong, Regularization theory and algorithm for some inverse problems for parabolic differential equations, PhD Dissertation, Lanzhou University, 2007. [40] X. T. Xiong, J. X. Wang and M. Li, An optimal method for fractional heat conduction problem backward in time, Appl. Anal., 2012, 91(4), 823–840. [41] X. T. Xiong, Q. Zhou and Y. C. Hon, An inverse problem for fractional diffusion equation in 2-dimensional case: Stability analysis and regularization, J. Math. Anal. Appl., 2012, 393, 185–199. [42] X. Xu, J. Cheng and M. Yamamoto, Carleman estimate for a fractional diffusion equation with half order and application, Appl. Anal., 2011, 90(9), 1355–1371. [43] F. Yang, Q. X. Sun and X. X. Li, Three Landweber iterative methods for solving the initial value problem of time-fractional diffusion wave equation on spherically symmetric domain, Inverse Probl. Sci. En., 2021, 29(12), 2306–2356. [44] F. Yang, Q. C. Wang and X. X. Li, Unknown source identification problem for space-time fractional diffusion equation: Optimal error bound analysis and regularization method, Inverse Probl. Sci. En., 2021, 29(12), 2040–2084. [45] S. P. Yang, X. T. Xiong and Y. Z. Han, A modified fractional Landweber method for a backward problem for the inhomogeneous time-fractional diffusion equation in a cylinder, Int. J. Comput. Math., 2020, 97, 2375–2393. [46] G. M. Zaslavsky, Fractional kinetic-equation for Hamiltonian chaos, Phys. D, 1994, 76, 110–122. [47] H. W. Zhang and X. J. Zhang, Generalized Tikhonov method for the final value problem of time-fractional diffusion equation, Int. J. Comput. Math., 2017, 94(1), 66–78. [48] Y. Zhang, M. M. Meerschaert and B. Baeumer, Particle tracking for time-fractional diffusion, Phy. Rev. E, 2008, 78, 036705. [49] G. H. Zheng and T. Wei, Spectral regularization method for a Cauchy problem of the time fractional advection-dispersion equation, J. Comput. Appl. Math., 2010, 233, 2631–2640. -
-
-
Figure 1.
The input data
$ w_x(0,t) $ -
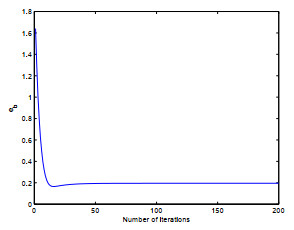
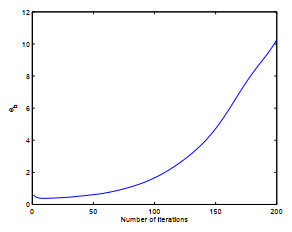
Figure 2.
The convergence error vs number of iterations for Example 4.1.
-
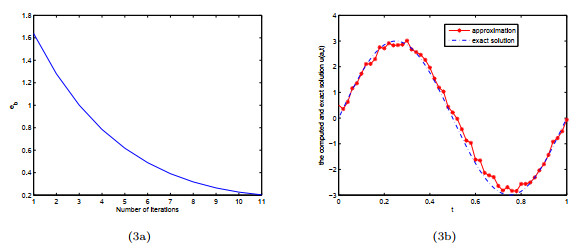
Figure 3.
(3a) The convergence error during the iterative process for Example 4.1; (3b) Reconstruction result with RMSE=0.23 and iterative step
$ k=11 $ -
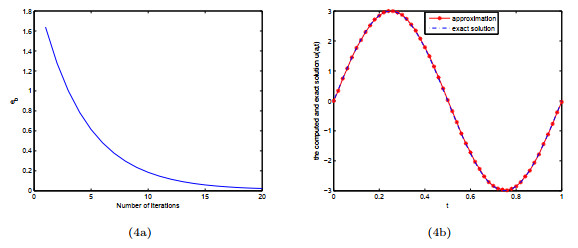
Figure 4.
(4a) The convergence error during the iterative process for Example 4.1; (4b) Reconstruction result with RMSE=0.023 and iterative step
$ k=20 $ -
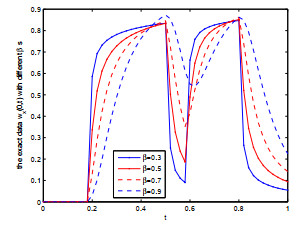
Figure 5.
The exact input data
$ w_x(0,t) $ $ \beta $ -
Figure 6.
The convergence error vs the number of iterations for Example 4.2.
-
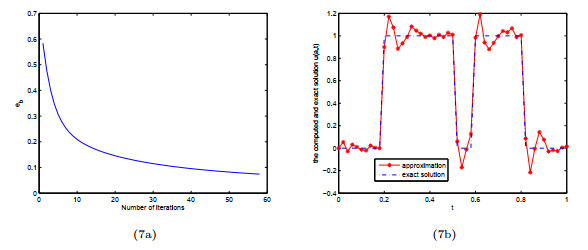
Figure 7.
(7a) The convergence error during the iterative process for Example 4.2; (7b) Reconstruction result with RMSE=0.07 and iterative step
$ k=50 $ -
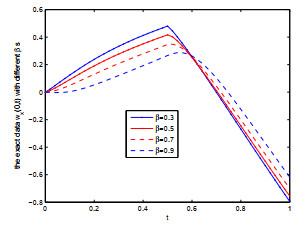
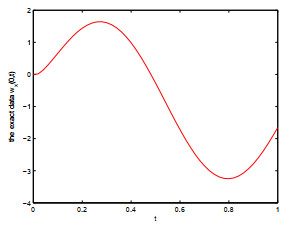
Figure 8.
The exact input data
$ w_x(0,t) $ $ \beta $ -
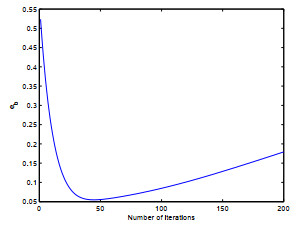
Figure 9.
The convergence error vs the number of iterations for Example 4.3.
-
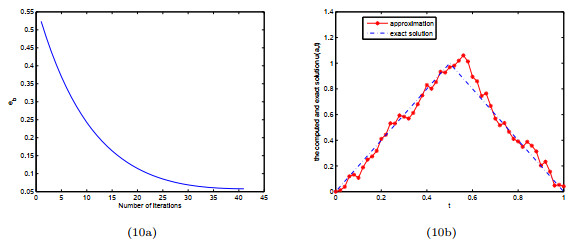
Figure 10.
(10a) The convergence error during the iterative process for Example 4.3; (10b) Reconstruction result with RMSE=0.06 and iterative step
$ k=40 $




 DownLoad:
DownLoad: