| Citation: |
Yanbo Chong, Fengde Chen. GLOBAL STABILITY, BIFURCATIONS AND CHAOS CONTROL IN A DISCRETE AMENSALISM MODEL WITH COVER AND SATURATION EFFECT[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2977-3003. doi: 10.11948/20240413
|
GLOBAL STABILITY, BIFURCATIONS AND CHAOS CONTROL IN A DISCRETE AMENSALISM MODEL WITH COVER AND SATURATION EFFECT
-
Abstract
In this paper, we propose a discrete amensalism model incorporating cover and saturation effect. The discrete model is derived from its continuous counterpart using the piecewise constant parameter method. First, we determine the equilibria, outline the conditions for their existence, and analyze their local stability properties. Subsequently, by employing discrete equation deflation and iteration methods, we establish a set of sufficient conditions that ensure the global attractivity of the system. Our analysis demonstrates that the size of the cover and the natural growth rate of the second population significantly influence the global attractivity of the system. Next, we investigate the existence of both flip bifurcation and transcritical bifurcation near the positive and boundary equilibria under certain conditions, utilizing the central manifold theorem and bifurcation theory. To control chaos arising from flip bifurcation, we implement feedback control strategies, specifically the hybrid control method. Finally, numerical simulations verify the feasibility of our theoretical results. Our research reveals that both the presence of cover and saturation effect enhance the density of the first population, while an increase in the amensalism coefficient $ c_1 $ ultimately leads to the extinction of the first population.
-
Keywords:
- Saturation effect /
- cover /
- global attractivity /
- flip bifurcation /
- transcritical bifurcation /
- chaos control
-
-
References
[1] Q. Cao, X. Bao and X. Yi, Dynamics of a predator-prey model with Allee effect and herd behavior, J. Nonl. Mod. Anal., 2024, 6(2), 392–412. [2] G. Chen and Z. Teng, On the stability in a discrete two-species competition system, J. Appl. Math. Comput., 2012, 38, 25–39. doi: 10.1007/s12190-010-0460-1 [3] Y. Chong, Y. Hou, S. Chen and F. Chen, The influence of fear effect to the dynamic behaviors of Lotka-Volterra ammensalism model, Eng. Lett., 32(6), 1233–1242. [4] Y. Chong, Y. Xue and S. Chen, Permanence of a discrete amensalism system with refuge and saturation effect, J. Ningde Norm. Univ.(Nat. Sci.), 2024, 36(1), 10–18. [5] Y. Chong, Q. Zhu, Q. Li and F. Chen, Dynamic behaviors of a two Species amensalism model with a second species dependent cover, Eng. Lett., 2024, 32(8), 1553–1561. [6] Q. Din and M. A. Zulfiqar, Qualitative behavior of a discrete predator–prey system under fear effects, Z. Naturforsch. A, 2022, 77(11), 1023–1043. doi: 10.1515/zna-2022-0129 [7] X. Du, X. Han and C. Lei, Chaos control and behavior analysis of a discrete-time dynamical system with competitive effect, J. Nonl. Mod. Anal., 2025, 7(1), 43–61. [8] Z. Fang, S. Chen and J. Wei, Global dynamics of a diffusive Leslie-Gower predator-prey model with fear effect, J. Nonl. Mod. Anal., 2022, 4(1), 129–140. [9] M. Feng, Y. Huang, S. Wang, et al., Properties of prodigiosin and its application in citrus preservation, Food Res. Dev., 2023, 44(22), 116–123. [10] W. Gao and B. Dai, Dynamics of a predator-prey model with delay and fear effect, J. Nonl. Mod. Anal., 2019, 1(1), 57–72. [11] K. Gopalsamy, Stability and Oscillations in Delay Differential Equations of Population Dynamics, Kluwer Academic, Boston, 1992. [12] X. Guan and F. Chen, Dynamical analysis of a two species amensalism model with Beddington-DeAngelis functional response and Allee effect on the second species, Nonlinear Anal. Real World Appl., 2019, 48, 71–93. doi: 10.1016/j.nonrwa.2019.01.002 [13] X. Guo, L. Ding, Y. Hui and X. Song, Dynamics of an amensalism system with strong Allee effect and nonlinear growth rate in deterministic and fluctuating environment, Nonlinear Dyn., 2024, 112, 21389–21408. doi: 10.1007/s11071-024-10158-0 [14] J. Hu and Z. Liu, Incorporating two coupling noises into a nonlinear competitive system with saturation effect, Int. J. Biomath., 2020, 13(02), 2050012. doi: 10.1142/S1793524520500126 [15] X. Hu, H. Li and F. Chen, Bifurcation analysis of a discrete amensalism model, Internat. J. Bifur. Chaos, 2024, 34(02), 2450020. doi: 10.1142/S0218127424500202 [16] M. Ibrahim, Global stability and bifurcation analysis of a Holling type Ⅱ amensalism model with harvesting: An optimal control approach, Available at SSRN, 2023, 28, 4489846. [17] H. Jiang and T. D. Rogers, The discrete dynamics of symmetric competition in the plane, J. Math. Biol., 1978, 25, 573–596. [18] X. Jin and X. Li, Dynamics of a discrete two-species competitive model with Michaelies-Menten type harvesting in the first species, J. Nonl. Mod. Anal., 2023, 5(3), 494–523. [19] Q. Li, J. K. Ankur, Q. Zhu and F. Chen, Dynamical behaviours of discrete amensalism system with fear effects on first species, Math. Biosci. Eng., 2024, 21(1), 832–860. [20] Q. Li, F. Chen, L. Chen and Z. Li, Dynamical analysis of a discrete amensalism system with Michaelis–Menten type harvesting for the second species, Qual. Theory Dyn. Syst., 2024, 23(1), 279. [21] Q. Li, Z. Liu and S. Yuan, Cross-diffusion induced Turing instability for a competition model with saturation effect, Appl. Math. Comput., 2019, 347, 64–77. [22] T. Li and Q. Wang, Bifurcation analysis for two-species commensalism (amensalism) systems with distributed delays, Internat. J. Bifur. Chaos, 2022, 32(09), 2250133. [23] D. Liaw, Application of center manifold reduction to nonlinear system stabilization, Appl. Math. Comput., 1998, 91(2–3), 243–258. [24] Z. Liu, R. Tan and Y. Chen, Modeling and analysis of a delayed competitive system with impulsive perturbations, Rocky Mt. J. Math., 2008, 38(5), 1505–1523. [25] Z. Lu, Q. Wu, J. Zhang and X. Mao, Antibacterial effect and mechanism of juglone from walnut green husk against Escherichia coli, Food Sci., 2023, 44(07), 65–73. [26] D. Luo and Q. Wang, Global dynamics of a Beddington-DeAngelis amensalism system with weak Allee effect on the first species, Appl. Math. Comput., 2021, 408, 126368. [27] X. Luo, G. Chen, B. Wang and J. Fang, Hybrid control of period-doubling bifurcation and chaos in discrete nonlinear dynamical systems, Chaos, Solitons & Fractals, 2003, 18, 775–783. [28] W. Ning, Z. Liu, L. Wang and R. Tan, Analysis of a stochastic competitive model with saturation effect and distributed delay, Methodol. Comput. Appl. Probab., 2021, 23, 1435–1459. [29] Rajni and B. Ghosh, Multistability, chaos and mean population density in a discrete-time predator-prey system, Chaos, Solitons & Fractals, 2022, 162, 112497. [30] A. Singh and V. S. Sharma, Bifurcations and chaos control in a discrete-time prey–predator model with Holling type-Ⅱ functional response and prey refuge, J. Comput. Appl. Math., 2023, 418, 114666. [31] M. Singh, Dynamical study and optimal harvesting of a two-species amensalism model incorporating nonlinear harvesting, Appl. Appl. Math., 2023, 18, 1. [32] B. Sita, K. L. Narayan and S. Bathul, A mathematical study of two species amensalism model with a cover for the first species by homotopy analysis method, Adv. Appl. Sci. Res, 2012, 3(3), 1821–1826. [33] G. Sun, Oualitative analysis on two populations amensalism model, J. Jiamusi Univ. (Nat. Sci. Ed.), 2003, 21(3), 284–286. [34] S. Tang, Y. Xiao, J. Liang and X. Wang, Mathematical biology, Science Press, Beijing, 2019, 55–59 (in Chinese). [35] Y. Wang, Dynamic behaviors of an amensalism system with density dependent birth rate, J. Nonlinear Funct. Anal., 2018, 2018, 1–9. [36] S. Winggins, Introduction to Applied Nonlinear Dynamical Systems and Chaos, Springer, Newyork, 2003. [37] R. Wu, L. Zhao and Q. Lin, Stability analysis of a two species amensalism model with Holling Ⅱ functional response and a cover for the first species, J. Nonlinear Funct. Anal., 2016, 2016, 1–15. [38] X. Xi, J. Griffin and S. Sun, Grasshoppers amensalistically suppress caterpillar performance and enhance plant biomass in an alpine meadow, Oikos, 2013, 122(7), 1049–1057. [39] X. Xie, F. Chen and M. He, Dynamic behaviors of two species amensalism model with a cover for the first species, J. Math. Comput. Sci., 2016, 16(3), 395–401. [40] R. Yang, Foundations of Modern Industrial Microbiology, Higher Edu. Press, Beijing, 2006. [41] X. Yang, Uniform persistence and periodic solutions for a discrete predator-prey system with delays, J. Math. Anal. Appl., 2006, 316, 161–177. [42] W. Yao and X. Li, Bifurcation difference induced by different discrete methods in a discrete predator-prey model, J. Nonl. Mod. Anal., 2022, 4(1), 64–79. [43] J. Zhang, Bifurcated periodic solutions in an amensalism system with strong generic delay kernel, Math. Methods Appl. Sci., 2013, 36(1), 113–124. [44] J. Zhang, Z Jin, J. Yan and G. Sun, Stability and Hopf bifurcation in a delayed competition system, Nonlinear Anal., 2009, 70, 658–670. [45] M. Zhao, Y. Ma and Y. Du, Global dynamics of an amensalism system with Michaelis-Menten type harvesting, Electron. Res. Arch., 2022, 31(2), 549–574. [46] Q. Zhou and F. Chen, Dynamical analysis of a discrete amensalism system with the Beddington-DeAngelis functional response and Allee effect for the unaffected species, Qual. Theory Dyn. Syst., 2023, 22(1), 16. [47] Q. Zhou, F. Chen and S. Lin, Complex dynamics analysis of a discrete amensalism system with a cover for the first species, Axioms, 2022, 11(8), 365. [48] Q. Zhou, Y. Chen, S. Chen and F. Chen, Dynamic analysis of a discrete amensalism model with Allee effect, J. Appl. Anal. Comput., 2023, 13(5), 2416–2432. [49] Q. Zhu, F. Chen, Z. Li and L. Chen, Global dynamics of two-species amensalism model with Beddington–DeAngelis functional response and fear effect, Internat. J. Bifur. Chaos, 2024, 34(06), 2450075. [50] Z. Zhu and Q. Chen, Mathematical analysis on amensalism Lotka-Volterra model of populations, J. Jixi Univ. (Nat. Sci. Ed.), 2008, 8(5), 100–101. -
-
Figures(9) / Tables(1)
Export File
Citation
Yanbo Chong, Fengde Chen. GLOBAL STABILITY, BIFURCATIONS AND CHAOS CONTROL IN A DISCRETE AMENSALISM MODEL WITH COVER AND SATURATION EFFECT[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2977-3003. doi: 10.11948/20240413
Format
Content
DownLoad:
-
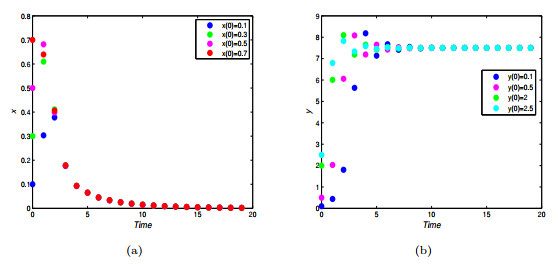
Figure 1.
Permanence of system (1.6), where
$ a_1=4,b_{1}=2,c_{1}=1,d_{1}=0.1, a_{2}=2.5,b_{2}=0.2,k=0.5, $ $ (x(0),y(0))=(0.8,3.5) $ -
Figure 2.
Permanence of system (1.6), where
$ a_1=1.5,b_{1}=1,c_{1}=1,d_{1}=0.5,a_{2}=0.5,b_{2}=0.2,k=0.5 $ $ (x(0),y(0))=(0.2,1),(0.4,1.6) $ $ (0.8, 3.5) $ -
Figure 3.
(a) Plot of population density
$ x $ $ y $ $ a_{1} $ $ b_{1}=1,c_{1}=1,d_{1}=0.5,a_{2}=0.5,b_{2}=0.2,k=0.5 $ $ E^{*} $ $ a_{1}=2.35,b_{1}=1,c_{1}=1,d_{1}=0.5,a_{2}=0.5,b_{2}=0.2,k=0.5 $ $ (x(0),y(0))=(0.5,0.3),(0.8 ,1) $ $ (2,3.2) $ -
Figure 4.
Global attractiveness of boundary equilibrium
$ E_{2} $ -
Figure 5.
Transcritical bifurcation diagram for boundary equilibrium
$ E_{2} $ -
Figure 6.
Plot of changes in amensalism coefficient
$ c_{1} $ $ x $ -
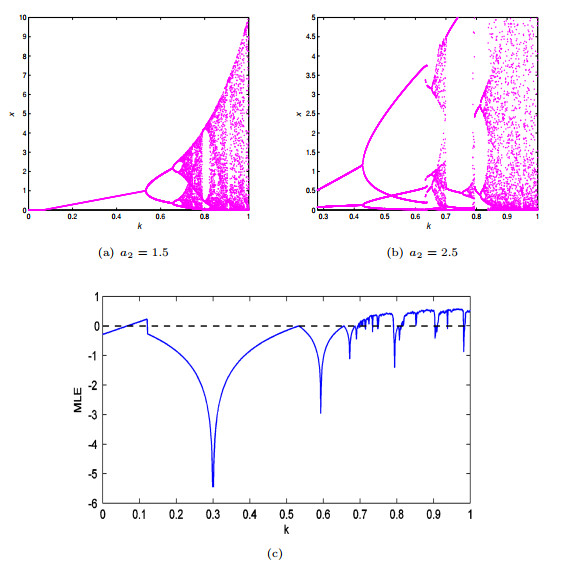
Figure 7.
Flip bifurcation and Maximal Lyapunov exponents maps.
-
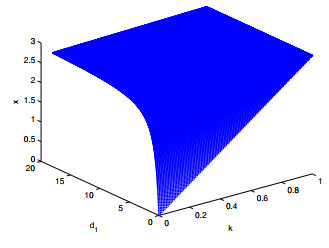
Figure 8.
Plot of
$ x^{*} $ $ k $ $ d_{1} $ -
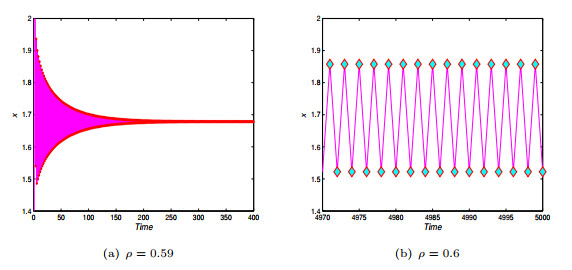
Figure 9.
Stability of the first population under different control parameters.