| Citation: | Haoran Geng, Liang Wang, Daqing Jiang. THRESHOLD BEHAVIOR OF A STOCHASTIC SVI EPIDEMIC MODEL WITH JUMP NOISE AND SATURATED INCIDENCE RATE[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 3004-3024. doi: 10.11948/20240455 |
THRESHOLD BEHAVIOR OF A STOCHASTIC SVI EPIDEMIC MODEL WITH JUMP NOISE AND SATURATED INCIDENCE RATE
-
Abstract
This paper analyzes a stochastic SVI epidemic model with jump noise and saturated incidence rate. By applying Kunita's inequality, we derive the asymptotic pathwise estimation of the stochastic solution. We then present the basic reproduction number of the model, $ \bar{R_0^{s}} $, which determines the extinction and persistence in the mean of the disease. Additionally, numerical simulations are conducted to verify the theoretical results. Consequently, both theoretical and numerical results indicate that the jump noise can hold off the spread of the disease.
-
Keywords:
- Stochastic SVI model /
- jump noise /
- Kunita’s inequality /
- threshold behavior /
- extinction
-

-
References
[1] D. Applebaum, Lévy Process and Stochastic Calculus, Cambridge Univ. Press, New York, 2009. [2] J. Bao, X. Mao, G. Yin and C. Yuan, Competitive Lotka–Volterra population dynamics with jumps, Nonlinear Anal. -Theor., 2011, 74(17), 6601–6616. doi: 10.1016/j.na.2011.06.043 [3] J. Bao and C. Yuan, Stochastic population dynamics driven by Lévy noise, J. Math. Anal. Appl., 2012, 391, 363–375. doi: 10.1016/j.jmaa.2012.02.043 [4] M. J. Beira and P. J. Sebastião, A differential equations model-fitting analysis of COVID-19 epidemiological data to explain multi-wave dynamics, Sci. Rep., 2021, 11, 16312. doi: 10.1038/s41598-021-95494-6 [5] B. Buonomo, G. Carbone and A. d'Onofrio, Effect of seasonality on the dynamics of an imitation-based vaccination model with public health intervention, Math. Biosci. Eng., 2018, 15, 299–321. [6] Z. Cao, W. Feng, X. Wen and L. Zu, Dynamical behavior of a stochastic SEI epidemic model with saturation incidence and logistic growth, Physica A, 2019, 523, 894–907. doi: 10.1016/j.physa.2019.04.228 [7] V. Capasso and G. Serio, A generalization of the Kermack-McKendrick deterministic epidemic model, Math. Biosci., 1978, 42, 43–61. doi: 10.1016/0025-5564(78)90006-8 [8] S. M. Imran, S. Asghar and M. Mushtaq, Mixed convection flow over an unsteady stretching surface in a porous medium with heat source, Math. Probl. Eng., 2012, 2012(1), 485418. doi: 10.1155/2012/485418 [9] H. Lee and A. Lao, Transmission dynamics and control strategies assessment of avian influenza A (H5N6) in the Philippines, Infect. Dis. Model., 2018, 3, 35–59. [10] D. Li, F. Wei and X. Mao, Stationary distribution and density function of a stochastic SVIR epidemic model, J. Franklin I., 2022, 359, 9422–9449. doi: 10.1016/j.jfranklin.2022.09.026 [11] G. B. Libotte, F. S. Lobato, G. M. Platt and A. J. S. Neto, Determination of an optimal control strategy for vaccine administration in COVID-19 pandemic treatment, Comput. Meth. Prog. Bio., 2020, 196, 105664. doi: 10.1016/j.cmpb.2020.105664 [12] R. S. Liptser, A strong law of large numbers for local martingales, Stochastics, 1980, 3, 217–228. doi: 10.1080/17442508008833146 [13] M. Liu and K. Wang, Dynamics of a two-prey one-predator system in random environments, J. Nonlinear Sci., 2013, 23, 751–775. doi: 10.1007/s00332-013-9167-4 [14] M. Liu and K. Wang, Dynamics of a Leslie–Gower Holling-type Ⅱ predator–prey system with Lévy jumps, Nonlinear Anal. -Theor., 2013, 85, 204–213. doi: 10.1016/j.na.2013.02.018 [15] Q. Liu, D. Jiang, T. Hayat and A. Alsaedi, Stationary distribution of a stochastic delayed SVEIR epidemic model with vaccination and saturation incidence, Physica A, 2018, 512, 849–863. doi: 10.1016/j.physa.2018.08.054 [16] D. Kiouach, Y. Sabbar and S. El Azami El‐idrissi, New results on the asymptotic behavior of an SIS epidemiological model with quarantine strategy, stochastic transmission, and Lévy disturbance, Math. Method. Appl. Sci., 2021, 44, 13468–13492. doi: 10.1002/mma.7638 [17] H. Kunita, Stochastic differential equations based on Lévy processes and stochastic flows of diffeomorphisms, Real and Stochastic Analysis: New Perspectives. Boston, MA: Birkhäuser Boston, 2004, 305–373. [18] X. Mao, Stochastic Differential Equations and Applications, Elsevier, 2007. [19] S. Peng and X. Zhu, Necessary and sufficient condition for comparison theorem of 1-dimensional stochastic differential equations, Stoch. Proc. Appl., 2006, 116, 370–380. doi: 10.1016/j.spa.2005.08.004 [20] N. Privault and L. Wang, Stochastic SIR Lévy jump model with heavy-tailed increments, J. Nonlinear Sci., 2021, 31, 1–28. doi: 10.1007/s00332-020-09667-0 [21] Z. Qiu, M. Y. Li and Z. Shen, Global dynamics of an infinite dimensional epidemic model with nonlocal state structures, J. Differ. Equations, 2018, 265, 5262–5296. doi: 10.1016/j.jde.2018.06.036 [22] X. Wang, K. Wang and Z. Teng, Global dynamics and density function in a class of stochastic SVI epidemic models with Lévy jumps and nonlinear incidence, AIMS Math., 2023, 8, 2829–2855. doi: 10.3934/math.2023148 [23] X. Yu and S. Yuan, Asymptotic properties of a stochastic chemostat model with two distributed delays and nonlinear perturbation, Discrete and Continuous Dynamical Systems - B, 2020, 25(7), 2373–2390. doi: 10.3934/dcdsb.2020014 [24] X. Zhang, D. Jiang, T. Hayat and B. Ahmad, Dynamical behavior of a stochastic SVIR epidemic model with vaccination, Physica A, 2017, 483, 94–108. doi: 10.1016/j.physa.2017.04.173 [25] Y. Zhao and D. Jiang, The threshold of a stochastic SIS epidemic model with vaccination, Appl. Math. Comput., 2014, 243, 718–727. [26] Y. Zhao and D. Jiang, The threshold of a stochastic SIS epidemic model with vaccination, Appl. Math. Comput., 2014, 243, 718–727. [27] B. Zhou, X. Zhang and D. Jiang, Dynamics and density function analysis of a stochastic SVI epidemic model with half saturated incidence rate, Chaos Soliton. Fract., 2020, 137, 109865. doi: 10.1016/j.chaos.2020.109865 [28] Y. Zhou and W. Zhang, Threshold of a stochastic SIR epidemic model with Lévy jumps, Physica A, 2016, 446, 204–216. doi: 10.1016/j.physa.2015.11.023 [29] Y. Zhu, L. Wang and Z. Qiu, Dynamics of a stochastic cholera epidemic model with Lévy process, Physica A, 2022, 595, 127069. [30] Y. Zhu, L. Wang and Z. Qiu, Threshold behaviour of a stochastic SIRS Lévy jump model with saturated incidence and vaccination, Math. Biosci. Eng., 2023, 20, 1402–1419. -
-
-
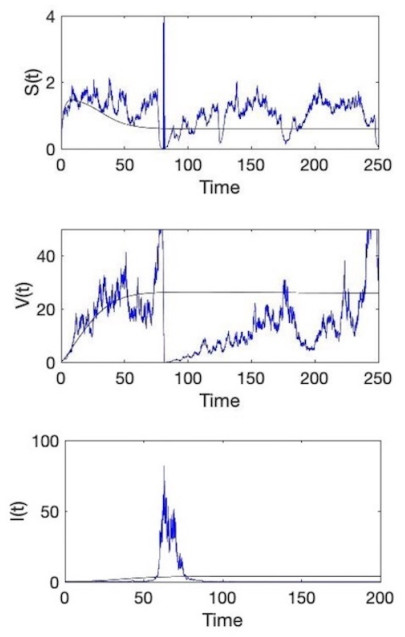
Figure 1.
The blue lines show the paths of
$ S(t), V(t), I(t) $ $ (\sigma_1^2,\sigma_2^2,\sigma_3^2)=(0.04,0.16,0.8),(\eta_1,\eta_2,\eta_3)=(0.1,0.1,0.1) $ -
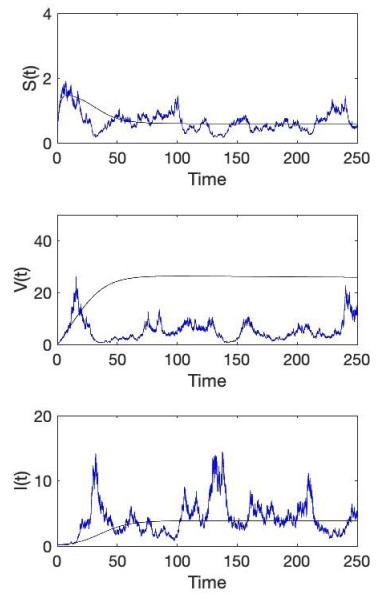
Figure 2.
The blue lines show the paths of
$ S(t), V(t), I(t) $ $ (\sigma_1^2,\sigma_2^2,\sigma_3^2)=(0.04,0.16,0.8),(\eta_1,\eta_2,\eta_3)=(0.1,0.1,0.8) $




 DownLoad:
DownLoad: