| Citation: | Hongyu Qin, Yuanyuan Li, Fengyan Wu. MAXIMUM ERROR ESTIMATES OF DISCONTINUOUS GALERKIN METHODS FOR SOLVING NEUTRAL DELAY DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2027-2043. doi: 10.11948/20240386 |
MAXIMUM ERROR ESTIMATES OF DISCONTINUOUS GALERKIN METHODS FOR SOLVING NEUTRAL DELAY DIFFERENTIAL EQUATIONS
-
Abstract
The exact solution to a neutral delay differential equation is generally non-smooth. Some possible loss of accuracy is usually found if certain high-order numerical methods are applied. The discontinuous Galerkin (DG) methods are introduced to numerically solve neutral delay differential equations so as to handle the difficulties. Maximum error estimates of the numerical method is investigated. Theoretical results indicate that the ${p}$-degree DG approximate solution has an accuracy of ${p}$-th order. Numerical experiments are presented to confirm the effectiveness and performance of the DG methods.
-

-
References
[1] S. Adjerid, K. Devine, J. Flaherty and L. Krivodonova, A posteriori error estimation for discontinuous Galerkin solutions of hyperbolic problems, Comput. Methods Appl. Mech. Engrg., 2002, 191, 1097–1112. doi: 10.1016/S0045-7825(01)00318-8 [2] A. Bellen and M. Zennaro, Numerical Methods for Delay Differential Equations, Oxford University Press, Oxford, 2003. [3] H. Brunner, Collocation Methods for Volterra Integral and Related Functional Differential Equations, Cambridge University Press, Cambridge, 2004. [4] H. Brunner and Q. Hu, Optimal superconvergence results for delay integro-differential equations of pantograph type, SIAM J. Numer. Anal., 2007, 45, 986–1004. doi: 10.1137/060660357 [5] H. Brunner, Q. Huang and H. Xie, Discontinuous Galerkin methods for delay differential equations of pantograph type, SIAM J. Numer. Anal., 2010, 48, 1944–1967. doi: 10.1137/090771922 [6] W. Cao, D. Li and Z. Zhang, Optimal superconvergence of energy conserving local discontinuous Galerkin methods for wave equations, Commu. Comput. Phys., 2017, 21, 211–236. doi: 10.4208/cicp.120715.100516a [7] W. Cao, D. Li and Z. Zhang, Superconvergence of discontinuous Galerkin methods based on upwind-biased fluxes for 1D linear hyperbolic equations, ESIAM Math. Model. Numer. Anal., 2017, 51(2), 467–486. doi: 10.1051/m2an/2016026 [8] Y. Cheng and C. W. Shu, Superconvergence of discontinuous Galerkin method and local discontinuous Galerkin schemes for linear hyperbolic and convection-diffusion equations in one space dimension, SIAM J. Numer. Anal., 2010, 47(6), 4044–4072. doi: 10.1137/090747701 [9] B. Cockburn, G. E. Karniadakis and C. W. Shu, The development of discontinuous Galerkin methods, in Discontinuous Galerkin Methods. Theory, Computation and Applications, Lecture Notes in Computational Science and Engineering, Springer-Verlag, 2000, 11, 3–50. [10] B. Cockburn and C. W. Shu, Foreword for the special issue on discontinuous Galerkin method, J. Sci. Comp., 2005, 22(23), 1–3. [11] Y. Cong, $NGP_{G}$-stability of linear multistep methods for systems of generalized neutral delay differential equations, Appl. Math. Mech., 2001, 22(7), 735–742. [12] Y. Cong, B. Yang and J. Kuang, Asymptotic stability and numerical analysis for systems of generalized neutral delay differential equations, Math. Numer. Sin., 2001, 23(4), 457–468. [13] Y. Cong, H. Zhao and Y. Zhang, Delay-dependent stability of multistep Runge-Kutta methods for delay differential systems of neutral type, J. Numer. Methods Comput. Appl., 2018, 39(4), 301–320. [14] C. Dawson, Special issue on discontinuous Galerkin methods, Comp. Meth. Appl. Mech. Eng., 2006, 195. [15] M. Delfour, W. Hager and F. Trochu, Discontinuous Galerkin methods for ordinary differential equations, Math. Comput., 1981, 36, 455–473. doi: 10.1090/S0025-5718-1981-0606506-0 [16] W. H. Enright and H. Hayashi, Convergence analysis of the solution of retarded and neutral delay differential equations by continuous numerical emthods, SIAM. J. Numer. Anal., 1998, 35(2), 572–585. doi: 10.1137/S0036142996302049 [17] D. Estep, A posteriori error bounds and global error control for approximations of ordinary differential equations, SIMA J. Numer. Anal., 1995, 32, 1–48. doi: 10.1137/0732001 [18] S. Gan, Dissipativity of $\theta$-methods for nonlinear delay differential equations of neutral type, Appl. Numer. Math., 2009, 59, 1354–1365. doi: 10.1016/j.apnum.2008.08.003 CrossRef $\theta$-methods for nonlinear delay differential equations of neutral type" target="_blank">Google Scholar
[19] H. Han and C. Zhang, Asymptotical-stability-preserving finite element methods in time for 2D neutral delay–reaction–diffusion equations, Appl. Math. Lett., 2022, 131, p. 108082. doi: 10.1016/j.aml.2022.108082 [20] P. Hu, C. Huang and S. Wu, Asymptotic stability of linear multistep methods for nonlinear neutral delay differential equations, Appl. Math. Comput., 2009, 211, 95–101. [21] Q. Huang, H. Xie and H. Brunner, Superconvergence of discontinuous Galerkin solutions for delay differential equations of pantograph type, SIAM J. Sci. Comput., 2011, 33, 2664–2684. doi: 10.1137/110824632 [22] Q. Huang, H. Xie and H. Brunner, The $hp$ discontinuous Galerkin method for delay differential equations with nonlinear vanishing delay, SIAM J. Sci. Comput., 2013, 35, 1614–1620. [23] A. Iserles, On the generalized pantograph functional-differential equation, Euro. J. Appl. Math., 1993, 4(1), 1–38. doi: 10.1017/S0956792500000966 [24] T. Koto, Stability of Runge-Kutta methods for the generalized pantograph equation, Numer. Math., 1999, 84, 233–247. doi: 10.1007/s002110050470 [25] D. Levy, C. W. Shu and J. Yan, Local discontinuous Galerkin methods for nonlinear dispersive equations, J. Comput. Phys., 2004, 196, 751–772. doi: 10.1016/j.jcp.2003.11.013 [26] D. Li and C. Zhang, Nonlinear stability of discontinuous Galerkin methods for delay differential equation, Appl. Math. Lett., 2010, 23, 457–461. doi: 10.1016/j.aml.2009.12.003 [27] D. Li and C. Zhang, Superconvergence of a discontinuous Galerkin method for first-order linear delay differential equations, J. Comp. Math., 2011, 29, 574–588. doi: 10.4208/jcm.1107-m3433 [28] D. Li and C. Zhang, $L^\infty$ error estimates of discontinuous Galerkin methods for delay differential equations, Appl. Numer. Math., 2014, 82, 1–10. doi: 10.1016/j.apnum.2014.01.008 CrossRef $L^\infty$ error estimates of discontinuous Galerkin methods for delay differential equations" target="_blank">Google Scholar
[29] D. Li, C. Zhang and H. Qin, LDG method for reaction–diffusion dynamical systems with time delay, Appl. Math. Comput., 2011, 217(22), 9173–9181. [30] Y. Li and Y. Li, Existence and exponential stability of almost periodic solution for neutral delay BAM neural net works with time-varying delays in leak age terms, J. Fran. Inst., 2013, 350, 2808–2825. doi: 10.1016/j.jfranklin.2013.07.005 [31] H. Qin, Q. Zhang and S. Wan, The continuous Galerkin finite element methods for linear neutral delay differential equations, Appl. Math. Comput., 2019, 346, 76–85. [32] D. Schötzau and C. Schwab, An $hp$ a priori error analysis of the DG time-stepping method for initial value problems, Calcolo, 2000, 37, 207–232. doi: 10.1007/s100920070002 CrossRef $hp$ a priori error analysis of the DG time-stepping method for initial value problems" target="_blank">Google Scholar
[33] D. Schötzau and C. Schwab, Time discretization of parabolic problems by the $hp$-version of discontinuous Galerkin finite element method, SIAM J. Numer. Anal., 2000, 38, 837–875. doi: 10.1137/S0036142999352394 CrossRef $hp$-version of discontinuous Galerkin finite element method" target="_blank">Google Scholar
[34] T. G. Seidel, S. V. Gurevich and J. Javaloyes, Conservative solitons and reversibility in time delayed systems, Phys. Rev. Lett., 2022, 128(8), p. 083901. [35] Q. Tu, Z. Li and L. Yi, Postprocessing technique of the discontinuous Galerkin method for solving delay differential equations, J. Appl. Math. Comput., 2024, 70, 3603–3630. doi: 10.1007/s12190-024-02114-3 [36] J. E. Vel$\acute{a}$zquez and V. L. Kharitonov, Lyapunov-Krasovskii functionals for scalar neutral type time delay equations, Sys. Cont. Lett., 2009, 58, 17–25. [37] A. G. Vladimirov and D. A. Dolinina, Neutral delay differential equation model of an optically injected Kerr cavity, Phys. Rev. E., 2024, 109(2), p. 024206. [38] W. S. Wang, Numerical Analysis of Nonlinear Neutral Functional Differential Equations, Ph. D. Thesis, 2008. [39] W. S. Wang, Optimal convergence orders of fully geometric mesh one-leg methods for neutral differential equations with vanishing variable delay, Adv. Comput. Math., 2019, 45(3), 1631–1655. [40] W. S. Wang and D. Li, Stability analysis of Runge-Kutta methods for nonlinear neutral Volterra delay-integro-differential equations, Numer. Math. Theo. Meth. Appl., 2011, 4, 537–561. [41] W. S. Wang and S. F. Li, Stability analysis of $\Theta$-method for nonlinear neutral functional differential equations, SIAM J. Sci. Comput., 2008, 30(4), 2181–2205. [42] W. S. Wang, S. F. Li and K. Su, Nonlinear stability of Runge-Kutta methods for neutral delay differential equations, J. Comput. Appl. Math., 2008, 214, 175–185. [43] W. S. Wang and C. Zhang, Analytical and numerical dissipativity for nonlinear generalized pantograph equations, Disc. Cont. Dyna. Syst., 2011, 29(3), 1245–1260. [44] W. S. Wang, Y. Zhang and S. F. Li, Nonlinear stability of one-leg methods for delay differential equations of neutral type, Appl. Numer. Math., 2008, 58, 122–130. [45] Z. Wang and Y. Cong, Delay-dependent stability of a class of Runge-Kutta methods for neutral differential equations, Numer. Algorithms, 2024, 1–24. [46] F. Wu, D. Li, J. Wen and J. Duan, Stability and convergence of compact finite difference method for parabolic problems with delay, Appl. Math. Comput., 2018, 322, 129–139. [47] S. Wu and T. Huang, Schwarz waveform relaxation for a neutral functional partial differential equation model of lossless coupled transmission lines, SIAM J. Sci. Comput., 2013, 35(2), 1161–1191. [48] Z. Xie and Z. Zhang, Uniform superconvergence analysis of the discontinuous Galerkin method for a singularity perturbed problem in 1-D, Math. Comput., 2010, 79, 35–45. [49] X. Xu and Q. Huang, Discontinuous Galerkin time stepping for semilinear parabolic problems with time constant delay, J. Sci. Comput., 2023, 96, 1–21. [50] J. Yan and C. W. Shu, A local discontinuous Galerkin method for KdV type equations, SIAM J. Numer. Anal., 2002, 40, 769–791. [51] G. Zhang and X. Dai, Superconvergence of discontinuous Galerkin method for neutral delay differential equations, Int. J. Comput. Math., 2021, 98(8), 1648–1662. [52] H. Zhu and Z. Zhang, Uniform convergence of the LDG method for a singularly perturbed problem with the exponential boundary layer, Math. Comput., 2014, 83, 635–663. -
-
-
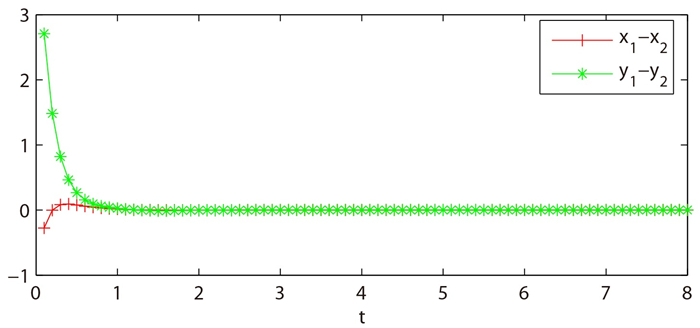
Figure 1.
The differences
$ x_1-x_2 $ $ y_1-y_2 $ $ 2 $




 DownLoad:
DownLoad: