| Citation: | Xiaowen Wu, Zhengge Huang. THE EFFECTIVE AND MODIFIED JACOBI GRADIENT BASED ITERATIVE ALGORITHMS FOR THE DISCRETE-TIME PERIODIC SYLVESTER MATRIX EQUATIONS[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2044-2088. doi: 10.11948/20240393 |
THE EFFECTIVE AND MODIFIED JACOBI GRADIENT BASED ITERATIVE ALGORITHMS FOR THE DISCRETE-TIME PERIODIC SYLVESTER MATRIX EQUATIONS
-
Abstract
In this paper, we discuss the new convergence properties of some gradient based iterative (GI) algorithms and propose two new GI-like algorithms for solving the discrete-time periodic Sylvester (DTPS) matrix equations and its generalized version, which often arise in the fields of physics, medicine and so forth. We first review the Jacobi GI (JGI) and accelerated JGI (AJGI) algorithms (Appl. Numer. Math., 168 (2021) 251-273) for the DTPS matrix equations, and establish the new and correct convergence conditions of these two algorithms. Then we apply a new update strategy to the JGI algorithm and develop the effective Jacobi gradient based iterative (EJGI) algorithm for solving the DTPS matrix equations, which is different from the AJGI one. Furthermore, based on the ideas of the JGI and the Gauss-Seidel (G-S) algorithms, we construct the modified Jacobi gradient based iterative (MJGI) algorithm for the generalized discrete-time periodic Sylvester (GDTPS) matrix equations. Compared with the JGI algorithm, the MJGI algorithm can make full use of the latest information to compute the next result and lead to a faster convergence rate. By utilizing the properties of the matrix norms, Kronecker product and techniques of inequalities, we prove that two proposed iterative algorithms are convergent under proper restrictions. Finally, some numerical examples are given to validate the efficiencies and advantages of the proposed EJGI and MJGI algorithms for DTPS and GDTPS matrix equations.
-

-
References
[1] S. Bittanti and P. Bolzern, Stabilizability and detectability of linear periodic systems, Syst. Control Lett., 1985, 6(2), 141–145. doi: 10.1016/0167-6911(85)90083-0 [2] S. Bittanti, P. Bolzern and P. Colaneri, Stability analysis of linear periodic systems via the Lyapunov equation, IFAC Proceedings Volumes, 1984, 17(2), 213–216. doi: 10.1016/S1474-6670(17)60971-6 [3] F. Ding, P.-X. Liu and J. Ding, Iterative solutions of the generalized Sylvester matrix equations by using the hierarchical identification principle, Appl. Math. Comput., 2008, 197(1), 41–50. [4] M. Hajarian, Extending LSQR methods to solve the generalized Sylvester-transpose and periodic Sylvester matrix equations, Math. Meth. Appl. Sci., 2014, 37(13), 2017–2028. doi: 10.1002/mma.2955 [5] M. Hajarian, A finite iterative method for solving the general coupled discrete-time periodic matrix equations, Circuits Syst. Signal Process., 2015, 34, 105–125. doi: 10.1007/s00034-014-9842-1 [6] M. Hajarian, Solving the general Sylvester discrete-time periodic matrix equations via the gradient based iterative method, Appl. Math. Lett., 2016, 52, 87–95. doi: 10.1016/j.aml.2015.08.017 [7] M. Hajarian, Matrix form of biconjugate residual algorithm to solve the discrete-time periodic Sylvester matrix equations, Asian J. Control, 2018, 20(1), 49–56. doi: 10.1002/asjc.1528 [8] M. Hajarian, Convergence properties of BCR method for generalized Sylvester matrix equation over generalized reflexive and anti-reflexive matrices, Linear Multilinear A., 2018, 66(10), 1975–1990. doi: 10.1080/03081087.2017.1382441 [9] M. Hajarian, Computing symmetric solutions of general Sylvester matrix equations via Lanczos version of biconjugate residual algorithm, Comput. Math. Appl., 2018, 76(4), 686–700. doi: 10.1016/j.camwa.2018.05.010 [10] M. Hajarian, Three types of biconjugate residual method for general periodic matrix equations over generalized bisymmetric periodic matrices, Trans. Inst. Meas. Control., 2019, 41(10), 2708–2725. doi: 10.1177/0142331218808859 [11] M. Hajarian, Reflexive periodic solutions of general periodic matrix equations, Math. Meth. Appl. Sci., 2019, 42(10), 3527–3548. doi: 10.1002/mma.5596 [12] Z.-H. He and Q.-W. Wang, A system of periodic discrete-time coupled Sylvester quaternion matrix equations, Algebra Colloquium, 2017, 24(01), 169–180. doi: 10.1142/S1005386717000104 [13] V. Hernanadez and A. M. Urbano, Pole-placement problem for discrete-time linear periodic systems, Int. J. Control, 1989, 50(1), 361–371. doi: 10.1080/00207178908953366 [14] B.-H. Huang and C.-F. Ma, The relaxed gradient-based iterative algorithms for a class of generalized coupled Sylvester-conjugate matrix equations, J. Frank. Inst., 2018, 355(6), 3168–3195. doi: 10.1016/j.jfranklin.2018.02.014 [15] Z.-G. Huang and J.-J. Cui, Modified and accelerated relaxed gradient-based iterative algorithms for the complex conjugate and transpose matrix equations, Numer. Algorithms, 2024, 97, 1955–2009. doi: 10.1007/s11075-024-01775-2 [16] H. M. Kim, Y. Kim and J. Meng, Newton Schulz method for solving nonlinear matrix equation $X^{p}+A^{*}XA=Q$, J. Korean Math. Soc., 2018, 55(6), 1529–1540. [17] M. Kono, Eigenvalue assignment in linear periodic discrete-time systems, Int. J. Control, 1980, 32(1), 149–158. doi: 10.1080/00207178008922850 [18] C.-X. Li and S.-L. Wu, The SHSS preconditioner for saddle point problems, J. Appl. Anal. Comput., 2023, 13(6), 3221–3230. [19] S.-H. Li and C.-F. Ma, Factor gradient iterative algorithm for solving a class of discrete periodic Sylvester matrix equations, J. Frank. Inst., 2022, 359(17), 9952–9970. doi: 10.1016/j.jfranklin.2022.09.041 [20] S. Longhi and R. Zulli, A note on robust pole assignment for periodic systems, IEEE Trans. Automat. Contr., 1996, 41(10), 1493–1497. doi: 10.1109/9.539431 [21] L.-L. Lv, J.-B. Chen, L. Zhang and F.-R. Zhang, Gradient-based neural networks for solving periodic Sylvester matrix equations, J. Frank. Inst., 2022, 359(18), 10849–10866. doi: 10.1016/j.jfranklin.2022.05.023 [22] L.-L. Lv, W.-Q. Lai and X.-Y. Liu, A parametric poles assignment algorithm for high-order linear discrete periodic systems, J. Frank. Inst., 2023, 360(16), 11855–11870. doi: 10.1016/j.jfranklin.2023.09.010 [23] L.-L. Lv, S.-Y. Tang and L. Zhang, Parametric solutions to generalized periodic Sylvester bimatrix equations, J. Frank. Inst., 2020, 357(6), 3601–3621. doi: 10.1016/j.jfranklin.2019.12.031 [24] L.-L. Lv, Z. Zhang, L. Zhang and X.-X. Liu, Gradient based approach for generalized discrete-time periodic coupled Sylvester matrix equations, J. Frank. Inst., 2018, 355(15), 7691–7705. doi: 10.1016/j.jfranklin.2018.07.045 [25] A. Shirilord and M. Dehghan, Iterative algorithm for a generalized matrix equation with momentum acceleration approach and its convergence analysis, J. Frank. Inst., 2024, 361, 107021. doi: 10.1016/j.jfranklin.2024.107021 [26] A. Shirilord and M. Dehghan, Solving a system of complex matrix equations using a gradient-based method and its application in image restoration, Numer. Algorithms, 2024. DOI: 10.1007/s11075-024-01856-2. [27] A. Shirilord and M. Dehghan, Iterative method for constrained systems of conjugate transpose matrix equations, Appl. Numer. Math., 2024, 198, 474–507. doi: 10.1016/j.apnum.2024.01.016 [28] A. Shirilord and M. Dehghan, Stationary Landweber method with momentum acceleration for solving least squares problems, Appl. Math. Lett., 2024, 157, 109174. doi: 10.1016/j.aml.2024.109174 [29] A. Varga, Periodic Lyapunov equations: Some applications and new algorithms, Int. J. Control, 1997, 67(1), 69–88. doi: 10.1080/002071797224360 [30] W.-L. Wang, G.-R. Qu and C.-Q. Song, Cyclic gradient based iterative algorithm for a class of generalized coupled Sylvester-conjugate matrix equations, J. Frank. Inst., 2023, 360(11), 7206–7229. doi: 10.1016/j.jfranklin.2023.05.026 [31] W.-L. Wang and C.-Q. Song, Iterative algorithms for discrete-time periodic Sylvester matrix equations and its application in antilinear periodic system, Appl. Numer. Math., 2021, 168, 251–273. doi: 10.1016/j.apnum.2021.06.006 [32] W.-L. Wang and C.-Q. Song, A novel iterative method for solving the coupled Sylvester-conjugate matrix equations and its application in antilinear system, J. Appl. Anal. Comput., 2023, 13(1), 249–274. [33] W.-L. Wang, C.-Q. Song and S.-P. Ji, Iterative solution to a class of complex matrix equations and its application in time-varying linear system, J. Appl. Math. Comput., 2021, 67, 317–341. doi: 10.1007/s12190-020-01486-6 [34] W.-L. Wang, C.-Q. Song and W.-L. Wang, A new BCR method for coupled operator equations with submatrix constraint, J. Appl. Anal. Comput., 2024, 14(4), 2002–2036. [35] A.-G. Wu, X. L. Zeng, G.-R. Duan and W.-J. Wu, Iterative solutions to the extended Sylvester-conjugate matrix equations, Appl. Math. Comput., 2010, 217(1), 130–142. [36] A.-G. Wu, Y. Zhang and Y.-Y. Qian, Complex Conjugate Matrix Equations, Science Press, Beijing, 2017. [37] Y.-N. Wu and M.-L. Zeng, On ADMM-based methods for solving the nearness symmetric solution of the system of matrix equations, J. Appl. Anal. Comput., 2021, 11(1), 227–241. [38] Y.-J. Xie and C.-F. Ma, The accelerated gradient based iterative algorithm for solving a class of generalized Sylvester-transpose matrix equation, Appl. Math. Comput., 2016, 273, 1257–1269. [39] T.-X. Yan and C.-F. Ma, An iterative algorithm for solving a class of generalized coupled Sylvester-transpose matrix equations over bisymmetric or skew-anti-symmetric matrices, J. Appl. Anal. Comput., 2020, 10(4), 1282–1310. [40] M. K. Zak and F. Toutounian, Nested splitting conjugate gradient method for matrix equation $AXB=C$ and preconditioning, Comput. Math. Appl., 2013, 66(3), 269–278. doi: 10.1016/j.camwa.2013.05.004 CrossRef $AXB=C$ and preconditioning" target="_blank">Google Scholar
[41] H.-M. Zhang, Reduced-rank gradient-based algorithms for generalized coupled Sylvester matrix equations and its applications, Comput. Math. Appl., 2015, 70(8), 2049–2062. doi: 10.1016/j.camwa.2015.08.013 [42] H.-M. Zhang, Gradient-based iterative algorithm for the extended coupled Sylvester matrix equations, 2017 29th Chinese Control And Decision Conference (CCDC). IEEE, 2017, 1562–1567. [43] H.-M. Zhang and H.-C. Yin, New proof of the gradient-based iterative algorithm for a complex conjugate and transpose matrix equation, J. Frank. Inst., 2017, 354(16), 7585–7603. [44] J.-J. Zhang, A note on the iterative solutions of general coupled matrix equation, Appl. Math. Comput., 2011, 217(22), 9380–9386. -
-
-
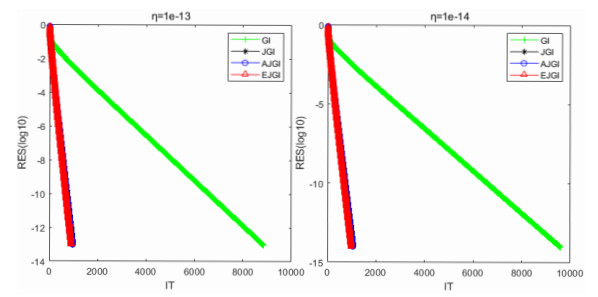
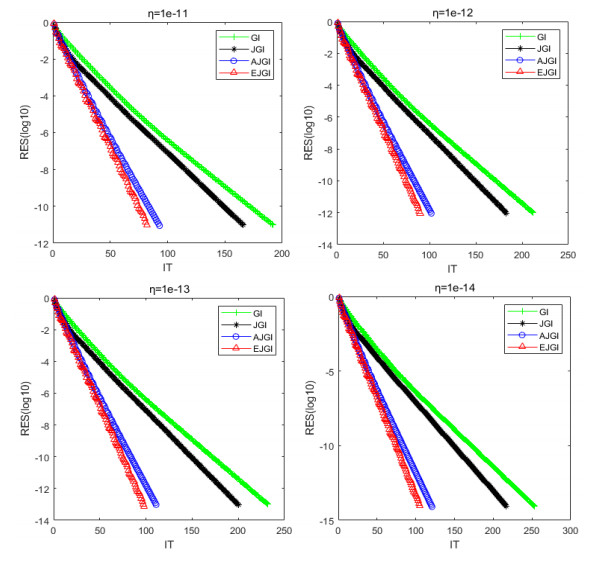
Figure 1.
Comparisons for the convergence curves of four GI-like algorithms for Example 6.1.
-
Figure 2.
Comparisons for the convergence curves of four GI-like algorithms for Example 6.1 with
$ \eta=10^{-13} $ $ \eta=10^{-14} $ -
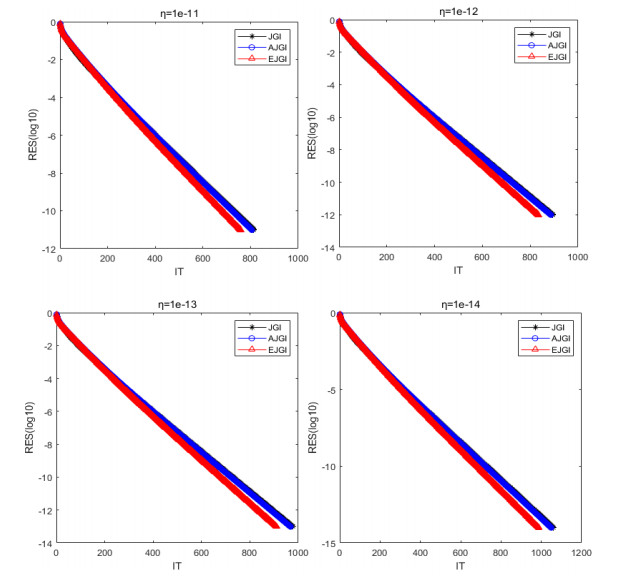
Figure 3.
Comparisons for the convergence curves of the JGI, AJGI and EJGI algorithms for Example 6.2.
-
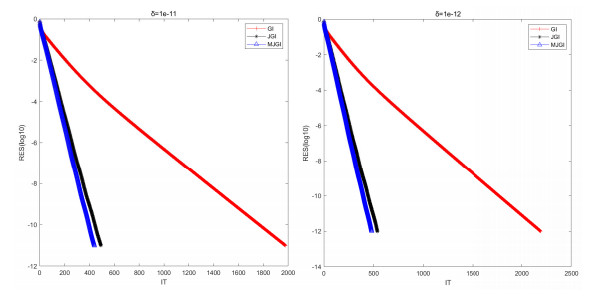
Figure 4.
Comparisons for the convergence curves of three GI-like algorithms for Example 6.3 with
$ \delta=10^{-11} $ $ \delta=10^{-12} $ -
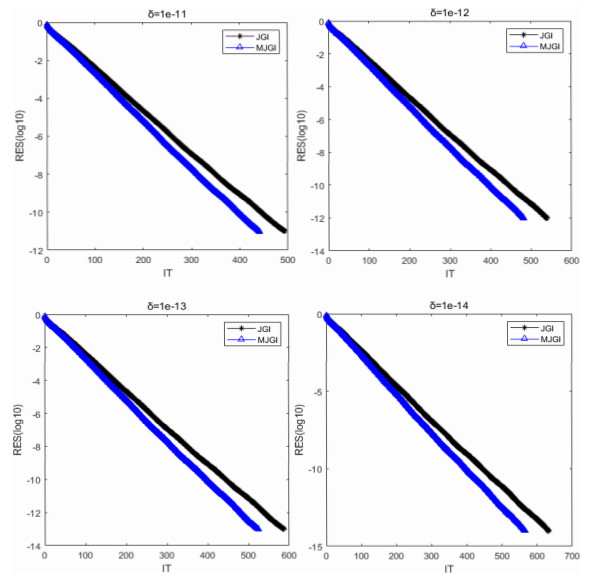
Figure 5.
Comparisons for the convergence curves of the JGI and MJGI algorithms for Example 6.3.




 DownLoad:
DownLoad: