| Citation: | Yindi Zhang, Meng Zhao. DYNAMICS OF AN SIRS EPIDEMIC MODEL WITH TIME DELAY AND FREE BOUNDARIES[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2258-2284. doi: 10.11948/20240435 |
DYNAMICS OF AN SIRS EPIDEMIC MODEL WITH TIME DELAY AND FREE BOUNDARIES
-
Abstract
In this paper, an SIRS epidemic model with time delay and free boundaries is studied. At first, we prove the global existence and uniqueness of the solution. And then we obtain criteria for spreading and vanishing. Moreover, the long-time behavior of the solution is given by a spreading-vanishing dichotomy. Finally, the numerical simulations are provided to illustrate our results. Our results indicate that the time delay can slow down the spreading of epidemic.
-
Keywords:
- An SIRS epidemic model /
- time delay /
- free boundary /
- spreading-vanishing dichotomy
-

-
References
[1] I. Ahn, S. Baek and Z. Lin, The spreading fronts of an infective environment in a man-environment-man epidemic model, Appl. Math. Model., 2016, 40(15–16), 7082–7101. doi: 10.1016/j.apm.2016.02.038 [2] R. M. Anderson and R. M. May, Population biology of infectious disease: Part I, Nature, 1979, 280(5721), 361–367. doi: 10.1038/280361a0 [3] E. Beretta, T. Hara and Y. Takeuchi, Global asymptotic stability of an SIR epidemic model with distributed time delay, Nonlinear Anal., 2001, 47(6), 4107–4115. doi: 10.1016/S0362-546X(01)00528-4 [4] J. F. Cao, Y. Du, F. Li and W. T. Li, The dynamics of a Fisher-KPP nonlocal diffusion model with free boundaries, J. Funct. Anal., 2019, 277(8), 2772–2814. doi: 10.1016/j.jfa.2019.02.013 [5] Q. Chen, F. Li, Z. Teng and F. Wang, Global dynamics and asymptotic spreading speeds for a partially degenerate epidemic model with time delay and free boundaries, J. Dynam. Differential Equations, 2022, 34(2), 1209–1236. doi: 10.1007/s10884-020-09934-4 [6] Q. Chen, S. Tang, Z. Teng and F. Wang, Spreading dynamics of a diffusive epidemic model with free boundaries and two delays, European J. Appl. Math., 2023, 34(6), 1133–1169. doi: 10.1017/S0956792523000220 [7] K. L. Cooke, Stability analysis for a vector disease model, Rocky Mountain J. Math., 1979, 9(1), 31–42. [8] K. L. Cooke and P. Van Den Driessche, Analysis of an SEIRS epidemic model with two delays, J. Math. Biol., 1996, 35(2), 240–260. doi: 10.1007/s002850050051 [9] Y. Du, Z. Guo and R. Peng, A diffusive logistic model with a free boundary in time-periodic enviroment, J. Funct. Anal., 2013, 265(9), 2089–2142. doi: 10.1016/j.jfa.2013.07.016 [10] Y. Du and Z. Lin, Spreading-vanishing dichotomy in the diffusive logistic model with a free boundary, SIAM J. Math. Anal., 2010, 42(1), 377–405. Erratum: SIAM J. Math. Anal., 2013, 45(3), 1995–1996. [11] Y. Du and Z. Lin, The diffusive competition model with a free boundary: Invasion of a superior or inferior competitor, Discrete Contin. Dyn. Syst. Ser. B, 2014, 19(10), 3105–3132. [12] A. Friedman, Partial Differential Equations of Parabolic Type, Prentice-Hall, Englewood Cliffs, N.J., 1964. [13] H. W. Hethcote and P. Van Den Driessche, Two SIS epidemiological models with delays, J. Math. Biol., 2000, 40: 2-26. doi: 10.1007/s002850050002 [14] Y. Hu, X. Hao, X. Song and Y. Du, A free boundary problem for spreading under shifting climate, J. Differential Equations, 2020, 269(7), 5931–5958. doi: 10.1016/j.jde.2020.04.024 [15] H. Huang and M. Wang, The reaction-diffusion system for an SIR epidemic model with a free boundary, Discrete Contin. Dyn. Syst. Ser. B, 2015, 20(7), 2039–2050. [16] H. Huang and M. Wang, A nonlocal SIS epidemic problem with double free boundaries, Z. Angew. Math. Phys., 2019, 70(4), 109. doi: 10.1007/s00033-019-1156-5 [17] W. O. Kermack and A. G. Mckendrick, A contribution to the mathematical theory of epidemics, Proc. Roy. Soc. London A, 1927, 115, 700-721. doi: 10.1098/rspa.1927.0118 [18] K. I. Kim, Z. Lin and Q. Zhang, An SIR epidemic model with free boundary, Nonlinear Anal. Real World Appl., 2013, 14(5), 1992-2001. doi: 10.1016/j.nonrwa.2013.02.003 [19] Y. N. Kyrychko and K. B. Blyuss, Global properties of a delayed SIR model with temporary immunity and nonlinear incidence rate, Nonlinear Anal. Real World Appl., 2005, 6(3), 495-507. doi: 10.1016/j.nonrwa.2004.10.001 [20] Y. N. Kyrychko and K. B. Blyuss, Stability and bifurcations in an epidemic model with varying immunity period, Bull. Math. Biol., 2010, 72(2), 490-505. doi: 10.1007/s11538-009-9458-y [21] L. Li, S. Liu and M. Wang, A viral propagation model with a nonlinear infection rate and free boundaries, Sci. China Math., 2021, 64(9), 1971-1992. doi: 10.1007/s11425-020-1680-0 [22] L. Li, W. Ni and M. Wang, Dynamical properties of a new SIR epidemic model, Discrete Contin. Dyn. Syst. Ser. S, 2023, 17(2), 690-707. [23] Z. Lin and H. Zhu, Spatial spreading model and dynamics of West Nile virus in birds and mosquitoes with free boundary, J. Math. Biol., 2017, 75(6-7), 1381-1409. doi: 10.1007/s00285-017-1124-7 [24] J. Liu, Z. Guo and Y. Li, Spreading dynamics of a biological invasion model with free boundaries and time delay, Nonlinear Anal. Real World Appl., 2024, 76, 103925. doi: 10.1016/j.nonrwa.2023.103925 [25] Z. Ma, M. Song and Y. Takeuchi, Global stability of an SIR epidemic model with time delay, Appl. Math. Lett., 2004, 17, 1141-1145. doi: 10.1016/j.aml.2003.11.005 [26] J. Mena-Lorcat and H. W. Hethcote, Dynamic models of infectious diseases as regulators of population sizes, J. Math. Biol., 1992, 30(7), 693-716. doi: 10.1007/BF00173264 [27] B. Sounvoravong, S. Guo and Y. Bai, Bifurcation and stability of a diffusive SIRS epidemic model with time delay, Electron. J. Differential Equations, 2019, 21-82(45), 1-16. [28] N. Sun and J. Fang, Propagation dynamics of Fisher-KPP equation with time delay and free boundaries, Calc. Var. Partial Differential Equations, 2019, 58(4). [29] Y. Tang, B. Dai and Z. Li, Dynamics of a Lotka-Volterra weak competition model with delays and free boundaries, Z. Angew. Math. Phys., 2022, 73(4), 143. doi: 10.1007/s00033-022-01788-8 [30] M. Wang, On some free boundary problems of the prey-predator model, J. Differential Equations, 2014, 256(10), 3365-3394. doi: 10.1016/j.jde.2014.02.013 [31] M. Wang, The diffusive logistic equation with a free boundary and sign-changing coefficient, J. Differential Equations, 2015, 258(4), 1252-1266. doi: 10.1016/j.jde.2014.10.022 [32] M. Wang, Existence and uniqueness of solutions of free boundary problems in heterogeneous environments, Discrete Contin. Dyn. Syst. Ser. B, 2019. 24(2): 415-421. Erratum: Discrete Contin. Dyn. Syst. Ser. B, 2021, 27(9), 5179-5180. [33] M. Wang and J. Zhao, Free boundary problems for a Lotka-Volterra competition system, J. Dynam. Differential Equations, 2014, 26(3), 655-672. doi: 10.1007/s10884-014-9363-4 [34] M. Wang and J. Zhao, A free boundary problem for the predator-prey model with double free boundaries, J. Dynam. Differential Equations, 2017, 29(3), 957-979. doi: 10.1007/s10884-015-9503-5 [35] R. Wang and Y. Du, Long-time dynamics of a diffusive epidemic model with free boundaries, Discrete Contin. Dyn. Syst. Ser. B, 2021, 26(4), 2201-2238. doi: 10.3934/dcdsb.2020360 [36] L. Wen and X. Yang, Global stability of a delayed SIRS model with temporary immunity, Chaos Solitons Fractals, 2008, 38(1), 221-226. doi: 10.1016/j.chaos.2006.11.010 [37] H. Xu, Z. Lin and H. Zhu, On an age-structured juvenile-adult model with harvesting pulse in moving and heterogeneous environment, J. Differential Equations, 2024, 405, 36-75. doi: 10.1016/j.jde.2024.05.045 [38] R. Xu, Z. Ma and Z. Wang, Global stability of a delayed SIRS epidemic model with saturation incidence and temporary immunity, Comput. Math. Appl., 2010, 59(9), 3211-3221. doi: 10.1016/j.camwa.2010.03.009 [39] M. Zhao, The longtime behavior of an SIR epidemic model with free boundaries, Journal of Nonlinear Modeling and Analysis, 2024, 6(2), 476-484. [40] M. Zhao, Dynamics of a reaction-diffusion waterborne pathogen model with free boundaries, Nonlinear Anal. Real World Appl., 2024, 77, 104043. doi: 10.1016/j.nonrwa.2023.104043 [41] D. Zhu, Y. Xu and X. Li, On a partially degenerate reaction-advection-diffusion system with free boundary conditions, J. Appl. Anal. Comput., 2025, 15(1), 21-38. -
-
-
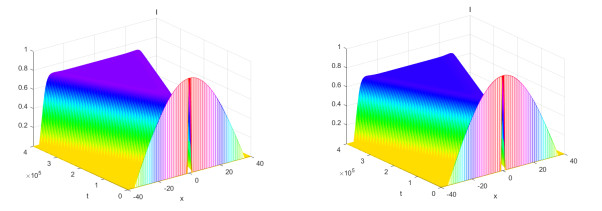
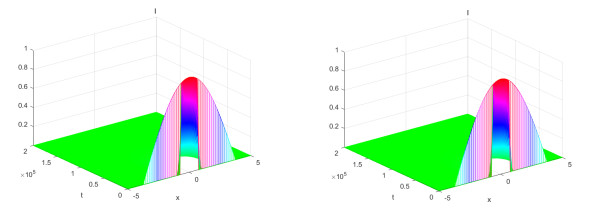
Figure 1.
The profiles of
$ \tau=0.5 $ $ \tau=0.8 $ -
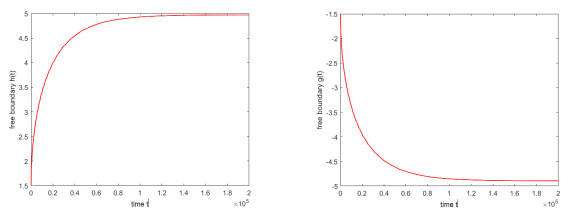
Figure 2.
Vanishing of the free boundary h(t) and g(t).
-
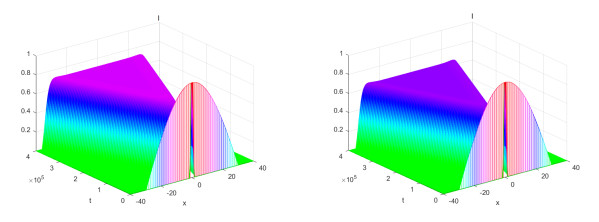
Figure 3.
The profiles of
$ \tau=0.5 $ $ \tau=0.8 $ -
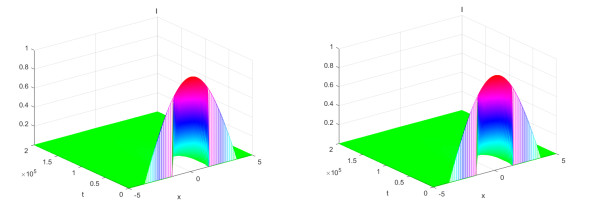
Figure 4.
The profiles of
$ \tau=0.5 $ $ \tau=0.8 $ $ \mu=10 $ -
Figure 5.
The profiles of
$ \tau=0.5 $ $ \tau=0.8 $ $ \mu=1 $ -
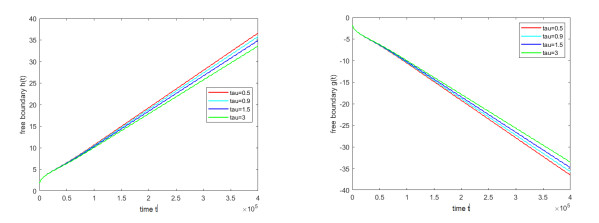
Figure 6.
Spreading of the free boundary
$ h(t) $ $ g(t) $




 DownLoad:
DownLoad: