| Citation: | Yuan Qin, Shuai Guo, Guangying Lv. NULL CONTROL OF CHAFEE-INFANTE EQUATIONS WITH SPATIALLY SCHEDULED ACTUATORS AND SENSORS[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2695-2713. doi: 10.11948/20240437 |
NULL CONTROL OF CHAFEE-INFANTE EQUATIONS WITH SPATIALLY SCHEDULED ACTUATORS AND SENSORS
-
Abstract
This paper addresses a switched sampled-data control design for stabilization of Chafee-Infante reaction-diffusion equation under Dirichlet boundary conditions with spatially scheduled actuators. The interval $[0, L]$ is divided into $N$ subdomains. It is assumed that discrete-time point-like or average measurements are available and $N$ sensors are placed in each subdomain and measure the average value of the state in the discrete time. The system is stabilized by switching sampled-data static output-feedback. A suitable control law for switching sampled-data is given. The proposed switching controller can be implemented either by placing $N$ actuators and sensors in each subdomain or by using an actuator-sensor pair that can move to the active subdomain. Constructive conditions are derived to ensure that the resulting closed-loop system is exponentially stable by means of the Lyapunov approach. Numerical example verifies our results.
-

-
References
[1] A. Armaou and P. Christofides, Feedback control of the Kuramoto-Sivashinsky equation, Phys. D., 2000, 137(1–2), 49–61. [2] A. Azouani and E. Titi, Feedback control of nonlinear dissipative systems by finite determining parameters-A reaction-diffusion paradigm, Evol. Equ. Control Theory, 2014, 3(4), 579–594. doi: 10.3934/eect.2014.3.579 [3] A. Bar and E. Fridman, Network-based distributed $H_\infty$-filtering of parabolic systems, Automatica J. IFAC, 2014, 50(12), 3139–3146. doi: 10.1016/j.automatica.2014.10.009 CrossRef $H_\infty$-filtering of parabolic systems" target="_blank">Google Scholar
[4] A. Butkovskiy and L. Pustyl'Nikov, Mobile Control of Distributed Parameter Systems, Chichester: Ellis Horwood Limited, 1987. [5] P. D. Christofides and A. Armaou, Global stabilization of the Kuramoto-Sivashinsky equation via distributed output feedback control, Systems Control Lett., 2000, 39(4), 283–294. doi: 10.1016/S0167-6911(99)00108-5 [6] M. A. Demetriou, Guidance of mobile actuator-plus-sensor networks for improved control and estimation of distributed parameter systems, IEEE Trans. Automat. Control, 2010, 55, 1570–1584. doi: 10.1109/TAC.2010.2042229 [7] M. A. Demetriou, Adaptive control of 2-D PDEs using mobile collocated actuator/sensor pairs with augmented vehicle dynamics, IEEE Trans. Automat. Control, 2012, 57, 2977–2978. doi: 10.1109/TAC.2012.2221169 [8] K. Ding, Q. Zhu and T. Huang, Prefixed-time local intermittent sampling synchronization of stochastic multicoupling delay reaction-diffusion dynamic networks, IEEE Trans. Neural Netw. Learn. Syst., 2024, 35(1), 718–732. doi: 10.1109/TNNLS.2022.3176648 [9] E. Fridman, Introduction to Time-Delay Systems: Analysis and Control, Basel: Birk$\ddot{a}$user, 2014. [10] E. Fridman and N. Bar Am, Sampled-data distributed $H_\infty$ control of transport reaction systems, SIAM J. Control Optim., 2013, 51(2), 1500–1527. doi: 10.1137/120867639 CrossRef $H_\infty$ control of transport reaction systems" target="_blank">Google Scholar
[11] E. Fridman and A. Blighovsky, Robust sampled-data control of a class of semilinear parabolic systems, Automatica J. IFAC, 2012, 48(5), 826–836. doi: 10.1016/j.automatica.2012.02.006 [12] D. Gilbarg and N. Trudinger, Elliptic Partial Differential Equations of Second Order, 2nd Ed., Springer-Verlag, New York, 1983. [13] D. Henry, Geometric Theory of Semilinear Parabolic Equations, New York: Springer-Verlag, 1981. [14] L. Hetel and E. Fridman, Robust sampled-data control of switched affine systems, IEEE Trans. Automat. Control, 2013, 58(11), 2922–2928. doi: 10.1109/TAC.2013.2258786 [15] O. Iftime and M. Demetriou, Optimal control of switched distributed parameter systems with spatially scheduled actuators, Automatica J. IFAC, 2009, 45(2), 312–323. doi: 10.1016/j.automatica.2008.07.012 [16] W. Kang and E. Fridman, Distributed sampled-data control of Kuramoto-Sivashinsky equation, Automatica J. IFAC, 2018, 95, 514–524. doi: 10.1016/j.automatica.2018.06.009 [17] W. Kang and E. Fridman, Sampled-data control of 2-D Kuramoto-Sivashinsky equation, IEEE Trans. Automat. Control, 2022, 67(3), 1314–1326. doi: 10.1109/TAC.2021.3070070 [18] W. Kang, E. Fridman and C. Liu, Stabilization by switching of parabolic PDEs with spatially scheduled actuators and sensors, Automatica J. IFAC, 2023, 147, Paper No. 110668, 10 pp. [19] M. Krasnoselskii, P. Zabreiko, E. Pustylii and P. Sobolevskii, Integral Operators in Spaces of Summable Functions, Springer Netherlands, 1976. [20] Z. Liao and Q. Lu, Stability estimate for an inverse stochastic parabolic problem of determining unknown time-varying boundary, Inverse Problems, 2024, 40(4), Paper No. 045032, 41 pp. [21] Q. Lu and Y. Wang, Null controllability for fourth order stochastic parabolic equations, SIAM J. Control Optim, 2022, 60(3), 1563–1590. doi: 10.1137/22M1472620 [22] E. Lunasin and E. Titi, Finite determining parameters feedback control for distributed nonlinear dissipative systems-a computational study, Evol. Equ. Control Theory, 2017, 6(4), 535–557. doi: 10.3934/eect.2017027 [23] A. Selivanov and E. Fridman, Delayed $H_\infty$ control of $2$D diffusion systems under delayed pointlike measurements, Automatica J. IFAC, 2019, 109, Article 108541. [24] M. Wang, M. Li and S. Huang, Unique continuation inequalities for nonlinear Schr$\ddot{o}$dinger equations based on uncertainty principles, Indiana Univ. Math. J., 2023, 72(1), 133–163. doi: 10.1512/iumj.2023.72.9135 CrossRef $\ddot{o}$dinger equations based on uncertainty principles" target="_blank">Google Scholar
[25] M. Wang and C. Zhang, Analyticity and observability for fractional order parabolic equations in the whole space, ESAIM Control Optim. Calc. Var., 2023, 29, Paper No. 63, 22 pp. [26] Y. Wang, Null controllability for stochastic coupled systems of fourth order parabolic equations, J. Math. Anal. Appl., 2024, 538(2), Paper No. 128426, 27 pp. [27] H. Wu and X. Zhang, Integrated design of switching control and mobile actuator/sensor guidance for a linear diffusion process, J. Franklin Inst., 2019, 356, 7246–7262. doi: 10.1016/j.jfranklin.2019.06.045 [28] H. Wu and X. Zhang, Static output feedback stabilization for a linear parabolic PDE system with time-varying delay via mobile collocated actuator/sensor pairs, Automatica J. IFAC, 2020, 117, 108993. [29] E. Zuazua, Switching control, J. Eur. Math. Soc., 2010, 13(1), 85–117. doi: 10.4171/jems/245 -
-
-
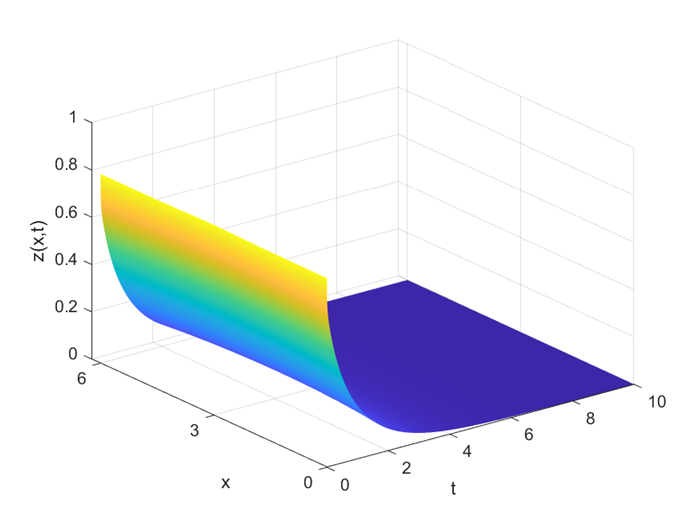
Figure 1.
State of unforced system.
-
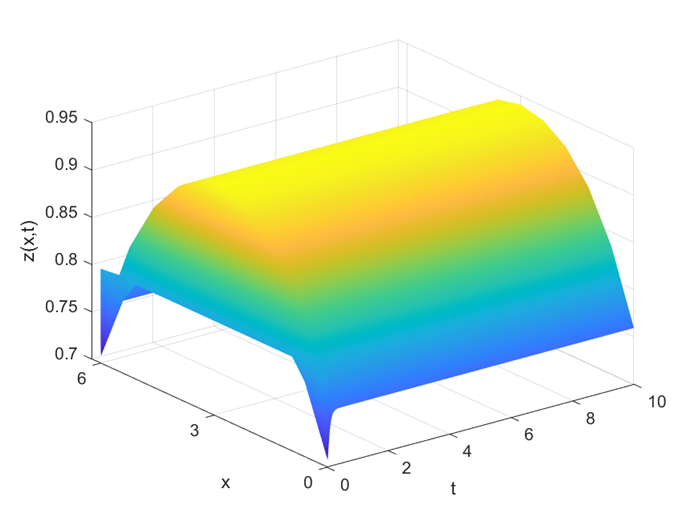
Figure 2.
State response of closed-loop system.
-
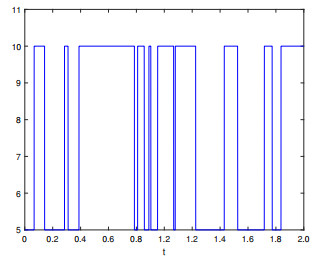
Figure 3.
Sensor/actuator locations:





 DownLoad:
DownLoad: