| Citation: |
Yuan Chang, Liqin Zhao. BIFURCATIONS OF LIMIT CYCLES IN A CLASS OF QUARTIC PLANAR VECTOR FIELDS[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2356-2380. doi: 10.11948/20240470
|
BIFURCATIONS OF LIMIT CYCLES IN A CLASS OF QUARTIC PLANAR VECTOR FIELDS
-
Abstract
This paper studies the number and the distribution of limit cycles of a class of planar quartic vector fields
$ \dot{x}=-y(ay^2-1)+\varepsilon p(x, y),\; \; \dot{y}=x(ax^2-\sqrt{a}x-1)+\varepsilon q(x, y), $
where $ a>0 $, $ 0<\varepsilon\ll 1 $, $ p(x,y) $ and $ q(x,y) $ are polynomials in $ (x,y) $ of the degree $ 4 $. By the bifurcation theory and qualitative analysis, we obtain four new configurations of limit cycles, two of which can have at least $ 12 $ limit cycles.
-
-
References
[1] Y. R. Carvalho, L. P. C. Da Cruz and L. F. S. Gouveia, New lower bound for the Hilbert number in low degree Kolmogorov systems, Chaos Solitons Fractals, 2023, 175, 113937. doi: 10.1016/j.chaos.2023.113937 [2] S. N. Chow, C. Li and D. Wang, Normal Forms and Bifurcation of Planar Vector Fields, Cambridge University Press, New York, 1994. [3] C. J. Christopher and N. G. Lloyd, Polynomial systems: A lower bound for the Hilbert numbers, Proc. Roy. Soc. London Ser. A, 1995, 450(1938), 219-224. doi: 10.1098/rspa.1995.0081 [4] R. D. Euzébio, J. Llibre and D. J. Tonon, Lower bounds for the number of limit cycles in a generalised Rayleigh-Liénard oscillator, Nonlinearity, 2022, 35(8), 3883-3906. doi: 10.1088/1361-6544/ac7691 [5] L. Gavrilov and I. D. Iliev, The limit cycles in a generalized Rayleigh-Liénard oscillator, Discrete Contin. Dyn. Syst., 2023, 43(6), 2381-2400. doi: 10.3934/dcds.2023014 [6] W. Geng, M. Han, Y. Tian and A Ke, Heteroclinic bifurcation of limit cycles in perturbed cubic Hamiltonian systems by higher-order analysis, J. Diff. Eqs., 2023, 357, 412-435. doi: 10.1016/j.jde.2023.02.027 [7] J. Giné, L. F. S. Gouveia and J. Torregrosa, Lower bounds for the local cyclicity for families of centers, J. Diff. Eqs., 2021, 275, 309-331. doi: 10.1016/j.jde.2020.11.035 [8] M. Han, Cyclicity of planar homoclinic loops and quadratic integrable systems, Sci. China Ser. A, 1997, 40(12), 1247-1258. doi: 10.1007/BF02876370 [9] M. Han and J. Chen, On the number of limit cycles in double homoclinic bifurcations, Sci. China Ser. A, 2000, 43(9), 914-928. doi: 10.1007/BF02879797 [10] M. Han, S. Hu and X. Liu, On the stability of double homoclinic and heteroclinic cycles, Nonlinear Anal., 2003, 53(5), 701-713. doi: 10.1016/S0362-546X(02)00301-2 [11] M. Han and J. Li, Lower bounds for the Hilbert number of polynomial systems, J. Diff. Eqs., 2012, 252, 3278-3304. doi: 10.1016/j.jde.2011.11.024 [12] M. Han, D. Shang, W. Zheng and P. Yu, Bifurcation of limit cycles in a fourth-order near-Hamiltonian system, Internat. J. Bifur. Chaos, 2007, 17(11), 4117-4144. doi: 10.1142/S0218127407019895 [13] M. Han, J. Yang and J. Li, General study on limit cycle bifurcation near a double homoclinic loop, J. Diff. Eqs., 2023, 347, 1-23. doi: 10.1016/j.jde.2022.11.031 [14] M. Han and Z. Zhang, Cyclicity 1 and 2 conditions for a 2-polycycle of integrable systems on the plane, J. Diff. Eqs., 1999, 155, 245-261. doi: 10.1006/jdeq.1998.3585 [15] C. Li, C. Liu and J. Yang, A cubic system with thirteen limit cycles, J. Diff. Eqs., 2009, 246, 3609-3619. doi: 10.1016/j.jde.2009.01.038 [16] J. Li, Hilbert's 16th problem and bifurcations of planar polynomial vector fields, Internat. J. Bifur. Chaos, 2003, 13(1), 47-106. doi: 10.1142/S0218127403006352 [17] J. Li and Y. Liu, New results on the study of $Z_q$-equivariant planar polynomial vector fields, Qual. Theory Dyn. Syst., 2010, 9(1-2), 167-219. doi: 10.1007/s12346-010-0024-7 [18] S. Liu and M. Han, Bifurcation theory of limit cycles by higher order Melnikov functions and applications, J. Diff. Eqs., 2024, 403, 29-66. doi: 10.1016/j.jde.2024.04.036 [19] J. Llibre, Some families of quadratic systems with at most one limit cycle, Bul. Acad. Ştiinţe Repub. Mold. Mat., 2023, 101(1), 8-15. [20] P. Yu and M. Han, Small limit cycles bifurcating from fine focus points in cubic order Z2-equivariant vector fields, Chaos Solitons Fractals, 2005, 24(1), 329-348. doi: 10.1016/S0960-0779(04)00599-5 [21] H. Zang, W. Chen and T. Zhang, Perturbation from a cubic Hamiltonian with three figure eight-loops, Chaos Solitons Fractals, 2004, 22(1), 61-74. doi: 10.1016/j.chaos.2003.12.061 [22] H. Zang, T. Zhang and M. Han, The number and distributions of limit cycles for a class of cubic near-Hamiltonian systems, J. Math. Anal. Appl., 2006, 316(2), 679-696. doi: 10.1016/j.jmaa.2005.04.085 [23] T. Zhang, M. Han, H. Zang and X. Meng, Bifurcations of limit cycles for a cubic Hamiltonian system under quartic perturbations, Chaos Solitons Fractals, 2004, 22(5), 1127-1138. doi: 10.1016/j.chaos.2004.03.028 -
-
Figures(5)
Export File
Citation
Yuan Chang, Liqin Zhao. BIFURCATIONS OF LIMIT CYCLES IN A CLASS OF QUARTIC PLANAR VECTOR FIELDS[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2356-2380. doi: 10.11948/20240470
Format
Content
DownLoad:
-
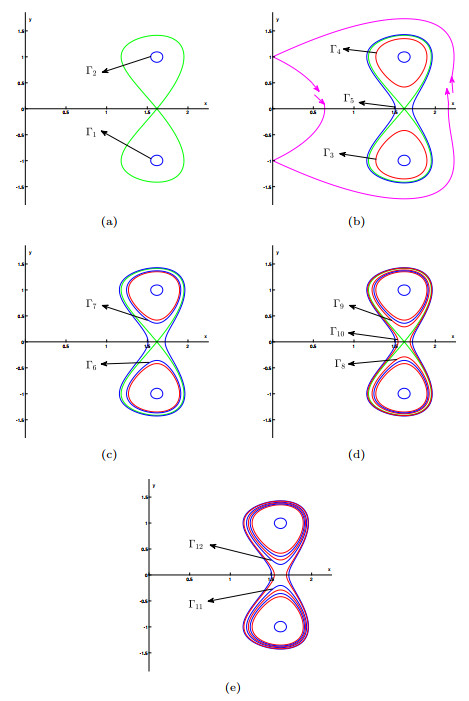
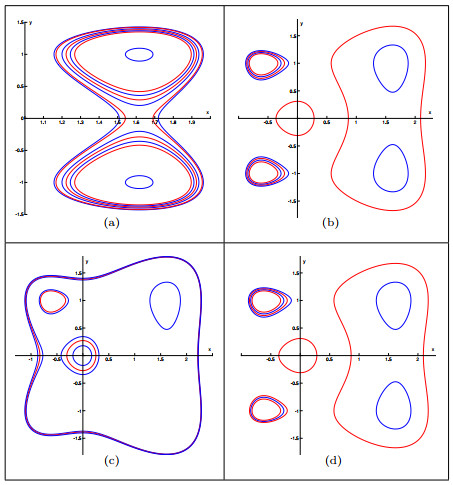
Figure 1.
(a), (b): The configuration of 12 limit cycles, (c) The configuration of 9 limit cycles, (d) The configuration of 11 limit cycles.
-
Figure 2.
The phase portrait of system (2.1).
-
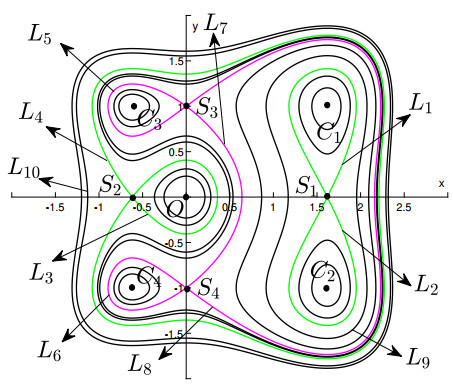
Figure 3.
The configuration of 12 limit cycles in Theorem 1.1(ⅰ).
-
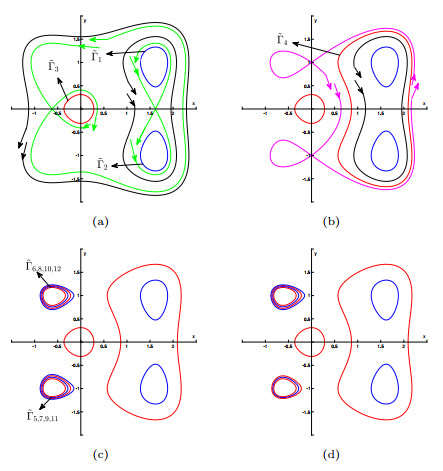
Figure 4.
The configuration of 12 or 11 limit cycles in Theorem 1.1(ⅱ).
-
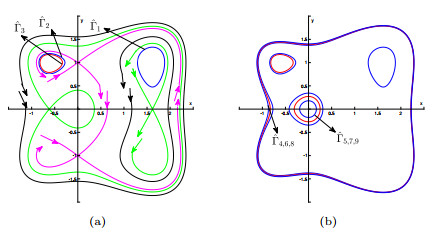
Figure 5.
The configuration of 9 limit cycles in Theorem 1.1(ⅲ).