| Citation: |
Haibo Luo, Weihua Sun. CONTROL OF JULIA SETS OF COURNOT-BERTRAND DUOPOLY GAME MODEL[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2427-2439. doi: 10.11948/20240489
|
CONTROL OF JULIA SETS OF COURNOT-BERTRAND DUOPOLY GAME MODEL
-
Abstract
Cournot-Bertrand duopoly game model is a very important model in the economic field. Based on the idea of feedback control, three controllers are designed to control Julia sets of Cournot-Bertrand duopoly game model in this study. The first method is the feedback control by use of the fixed point, the second is based on feedback control and cumulative error and the third is designed based on the feedback control and difference. The efficacy of three control methods is illustrated in simulations.
-
Keywords:
- Julia set /
- feedback control /
- Cournot-Bertrand duopoly game model
-
-
References
[1] G. Abdul Baki and W. Marrouch, Environmental taxation in the Bertrand differentiated duopoly: New insights, Resource and Energy Economics, 2022, 70, 101329. doi: 10.1016/j.reseneeco.2022.101329 [2] E. Ahmed, A. A. Elsadany and T. Puu, On Bertrand duopoly game with differentiated goods, Applied Mathematics and Computation, 2015, 251, 169–179. doi: 10.1016/j.amc.2014.11.051 [3] J. Andaluz, A. A. Elsadany and G. Jarne, Dynamic behavior in a Cournot duopoly with social responsibility, Chaos, Solitons & Fractals, 2023, 172, 113511. [4] A. Arya, B. Mittendorf and D. E. M. Sappington, Outsourcing, vertical integration, and price vs. Quantity competition, International Journal of Industrial Organization, 2008, 26(1), 1–16. doi: 10.1016/j.ijindorg.2006.10.006 [5] C. Beck, Physical meaning for Mandelbrot and Julia sets, Physica D: Nonlinear Phenomena, 1999, 125(3–4), 171–182. doi: 10.1016/S0167-2789(98)00243-7 [6] E. Cumbul, Stackelberg versus Cournot oligopoly with private information, International Journal of Industrial Organization, 2021, 74, 102674. doi: 10.1016/j.ijindorg.2020.102674 [7] E. Dalla, Asymmetries in banking conduct: A Cournot-Bertrand model, Economics Letters, 2023, 233, 111426. doi: 10.1016/j.econlet.2023.111426 [8] B. Du, C. Wu, G. Zhang and X.-L. Zhou, Dynamical behaviors of a discrete two-dimensional competitive system exactly driven by the large centre, Journal of Applied Analysis & Computation, 2024, 14(5), 2822–2844. [9] K. Falconer, Fractal Geometry: Mathematical Foundation and Application, Wiley Press, West Chester, UK, 2013. [10] N. Garcia-Vicente, D. D. Garcia-Swartz and M. Campbell-Kelly, What do we know about duopolies? Insights from the history of cellular phones, Telecommunications Policy, 2022, 46(2), 102259. doi: 10.1016/j.telpol.2021.102259 [11] Ö. AK Gümüş, A study on stability, bifurcation analysis and chaos control of a discrete-time prey-predator system involving Allee effect, Journal of Applied Analysis & Computation, 2023, 13(6), 3166–3194. [12] G. Julia, Mémoire sur l'itération des fonctions rationnelles, Journal de Mathématiques Pures et Appliquées, 1918, 1, 47–246. [13] X. Li and Y. Jiang, Influence of rationality levels on dynamics of heterogeneous Cournot duopolists with quadratic costs, Heliyon, 2023, 9(12), e22827. doi: 10.1016/j.heliyon.2023.e22827 [14] N. Selem Mojica, J. Navarro, P. C. Marijuán and R. Lahoz-Beltra, Cellular "bauplans": Evolving unicellular forms by means of Julia sets and Pickover biomorphs, Biosystems, 2009, 98(1), 19–30. doi: 10.1016/j.biosystems.2009.07.002 [15] A. Mukherjee, L. F. S. Wang and J. Sun, Bertrand-Cournot profit reversal in a vertical structure with cross ownership, Economics Letters, 2024, 238, 111681. doi: 10.1016/j.econlet.2024.111681 [16] A. Quadir, Demand information sharing in Cournot-Bertrand model, Operations Research Letters, 2024, 53, 107069. doi: 10.1016/j.orl.2024.107069 [17] G. Sarafopoulos and K. Papadopoulos, Complexity of a Bertrand duopoly game with homogeneous expectations, quadratic cost functions and chaos control, IFAC-PapersOnLine, 2021, 54(17), 41–46. doi: 10.1016/j.ifacol.2021.11.024 [18] A. Semenov and J.-B. Tondji, On the dynamic analysis of Cournot–Bertrand equilibria, Economics Letters, 2019, 183, 108549. doi: 10.1016/j.econlet.2019.108549 [19] J. Shu and Y. Zhang, Fractal control and synchronization of population competition model based on the T–S fuzzy model, Chaos, Solitons & Fractals, 2023, 172, 113583. [20] C. Sun and F.-C. Lai, Spatial price discrimination in a symmetric barbell model: Bertrand vs. Cournot, Papers in Regional Science, 2014, 93(1), 141–159. doi: 10.1111/j.1435-5957.2012.00476.x [21] J. Sun, W. Qiao and S. Liu, New identification and control methods of sine-function Julia sets, Journal of Applied Analysis & Computation, 2015, 5(2), 220–231. [22] W. Sun and Y. Zhang, Control and synchronization of Julia sets in the forced brusselator model, International Journal of Bifurcation and Chaos, 2015, 25(09), 1550113. doi: 10.1142/S0218127415501138 [23] Y. Sun, R. Xu, L. Chen, et al., Image compression and encryption scheme using farcatal dictionary and Julia set, IET Image Processing, 2015, 9(3), 173–183. doi: 10.1049/iet-ipr.2014.0224 [24] C. H. Tremblay and V. J. Tremblay, The Cournot–Bertrand model and the degree of product differentiation, Economics Letters, 2011, 111(3), 233–235. doi: 10.1016/j.econlet.2011.02.011 [25] V. J. Tremblay, C. H. Tremblay and K. Isariyawongse, Cournot and Bertrand competition when advertising rotates demand: The case of Honda and Scion, International Journal of the Economics of Business, 2013, 20(1), 125–141. doi: 10.1080/13571516.2012.750045 [26] C. Wang, J. Pi, D. Zhou, W. Tang and G. Yang, Dynamics of n-person Cournot games with asymmetric information and heterogeneous expectations, Physica A: Statistical Mechanics and Its Applications, 2023, 618, 128691. doi: 10.1016/j.physa.2023.128691 [27] D. Wang, S. Liu, K. Liu and Y. Zhao, Control and synchronization of Julia sets generated by a class of complex time-delay rational map, Journal of Applied Analysis & Computation, 2016, 6(4), 1049–1063. [28] H. Wang and J. Ma, Complexity analysis of a Cournot-Bertrand duopoly game model with limited information, Discrete Dynamics in Nature and Society, 2013, 2013, 1–6. [29] Y. Wang, S. Liu and W. Wang, Fractal dimension analysis and control of Julia set generated by fractional Lotka–Volterra models, Communications in Nonlinear Science and Numerical Simulation, 2019, 72, 417–431. doi: 10.1016/j.cnsns.2019.01.009 [30] X. Xiang and B. Cao, Multidimensional game of Cournot-Bertrand model with incomplete information and its analysis, Procedia Engineering, 2012, 29, 895–902. doi: 10.1016/j.proeng.2012.01.061 [31] P. Zanchettin, Differentiated duopoly with asymmetric costs, Journal of Economics & Management Strategy, 2006, 15(4), 999–1015. [32] Y. Zhang and S. Liu, Gradient control and synchronization of Julia sets, Chinese Physics B, 2008, 17(2), 543–549. doi: 10.1088/1674-1056/17/2/032 [33] Y. Zhu, W. Zhou, T. Chu and A. A. Elsadany, Complex dynamical behavior and numerical simulation of a Cournot-Bertrand duopoly game with heterogeneous players, Communications in Nonlinear Science and Numerical Simulation, 2021, 101, 105898. doi: 10.1016/j.cnsns.2021.105898 -
-
Figures(7)
Export File
Citation
Haibo Luo, Weihua Sun. CONTROL OF JULIA SETS OF COURNOT-BERTRAND DUOPOLY GAME MODEL[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2427-2439. doi: 10.11948/20240489
Format
Content
DownLoad:
-
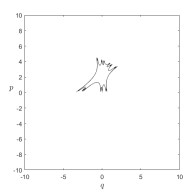
Figure 1.
Julia sets for model (2.1) when
$ \alpha= 2.05 $ $ \beta=0.2 $ $ c=2.7 $ $ d= 0.8 $ -
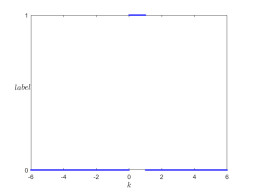
Figure 2.
Estimation of the distribution range of values of k that stabilize the fixed point.
-
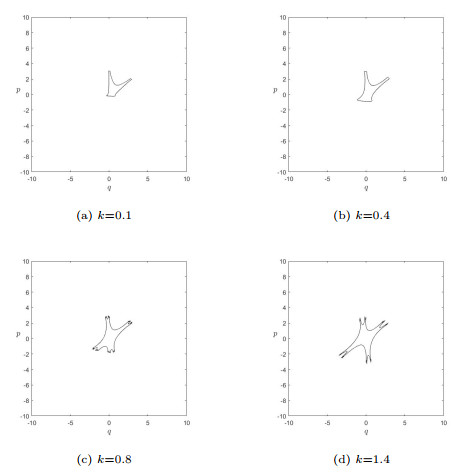
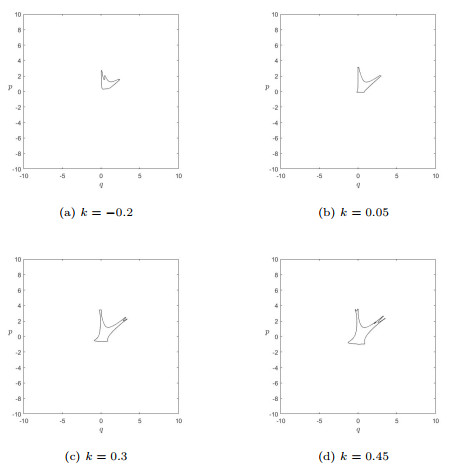
Figure 3.
Variation of Julia sets of the controlled system (3.3) with control parameter k.
-
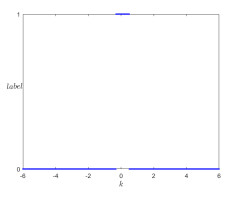
Figure 4.
Estimation of the distribution range of values of k that make the fixed point
$ (q^*,p^*,0,0) $ -
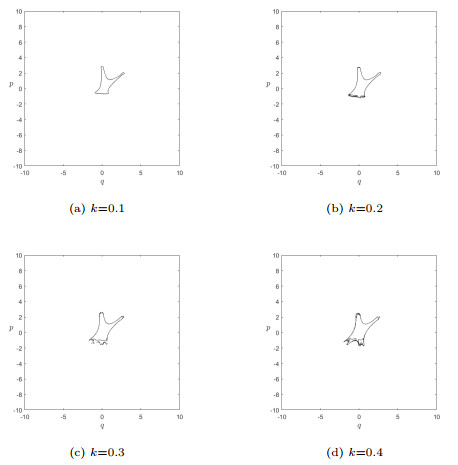
Figure 5.
Variation of Julia sets of the controlled system (3.5) with control parameter k.
-
Figure 6.
Estimation of the distribution range of values of k that make the fixed point be stable.
-
Figure 7.
Variation of Julia sets of the controlled system (3.8) with control parameter k.