| Citation: |
Xiaoxiao Zheng, Xiaolin Si, Yanxiao Lu. NEW TRAVELING WAVE SOLUTIONS OF THE (3+1)-DIMENSIONAL GENERALIZED BREAKING SOLITON EQUATION[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 3045-3066. doi: 10.11948/20240520
|
NEW TRAVELING WAVE SOLUTIONS OF THE (3+1)-DIMENSIONAL GENERALIZED BREAKING SOLITON EQUATION
-
Abstract
In this paper, we will study solutions of the (3+1)-dimensional generalized breaking soliton (gBS) equation which used to describe the interaction phenomena between Riemann wave and long wave via three space variables in nonlinear media. Firstly, we transform (3+1)-dimensional gBS equation to the bilinear form. Secondly, we apply the three-wave method to study bilinear form and then get many kinds of solutions for (3+1)-dimensional gBS equation, concluding periodic solitary wave solutions, bell solitary wave solutions, two-soliton solutions, breather lump wave solutions, et al. These solutions can describe interaction between waves and are presented by 3D and 2D graphs. Finally, we analyze the resolving thoughts of extended homoclinic test method and its correlation of three-wave method. Our results show the significance and efficiency of these methods.
-
-
References
[1] Abdullah, A. R. Seadawy and J. Wang, Mathematical methods and solitary wave solutions of three-dimensional zakharov-kuznetsov-burgers equation in dusty plasma and its applications, Results Phys., 2017, 7, 4269–4277. doi: 10.1016/j.rinp.2017.10.045 [2] T. Assiotis, Exact solution of interacting particle systems related to random matrices, Commun. Math. Phys., 2023, 402(3), 2641–2690. doi: 10.1007/s00220-023-04777-8 [3] R. D. Chen, Y. T. Gao, T. T. Jia, et al., Periodic-wave solutions and asymptotic properties for a (3+1)-dimensional generalized breaking soliton equation in fluids and plasmas, Modern Phys. Lett. B, 2021, 35(20), 2150344. doi: 10.1142/S0217984921503449 [4] Y. Chen, X. Lü and X. L. Wang, B$\ddot{a}$cklund transformation, wronskian solutions and interaction solutions to the (3+1)-dimensional generalized breaking soliton equation, Eur. Phys. J. Plus., 2023, 138(6), 492. doi: 10.1140/epjp/s13360-023-04063-5 [5] R. Cherniha and V. Davydovych, Symmetries and exact solutions of the diffusive holling-tanner prey-predator model, Acta Appl. Math., 2023, 187(1), 8. doi: 10.1007/s10440-023-00600-7 [6] J. Y. Cui, D. L. Li and T. F. Zhang, Symmetry reduction and exact solutions of the (3+1)-dimensional nKdV-nCBS equation, Appl. Math. Lett., 2023, 144, 108718. doi: 10.1016/j.aml.2023.108718 [7] M. T. Darvishi and M. Najafi, A modification of extended homoclinic test approach to solve the (3+1)-dimensional potential-ytsf equation, Chinese Phys. Lett., 2011, 28(4), 040202. doi: 10.1088/0256-307X/28/4/040202 [8] L. T. Gai, W. X. Ma and M. C. Li, Lump-type solutions, rogue wave type solutions and periodic lump-stripe interaction phenomena to a (3+1)-dimensional generalized breaking soliton equation, Phys. Lett. A, 2020, 384, 126178. doi: 10.1016/j.physleta.2019.126178 [9] L. T. Gai, W. Y. Wu, T. F. Ding, et al., Lump wave solutions, lump-stripe soliton inelastic collision phenomena and rogue-type wave solutions for a generalized breaking soliton system in (3+1)-dimensions, Wave Motion, 2024, 124, 103243. doi: 10.1016/j.wavemoti.2023.103243 [10] K. Hosseini, E. Hincal, F. Alizadeh, et al., Bifurcation analysis, sensitivity analysis, and Jacobi elliptic function structures to a generalized nonlinear Schrödinger equation, Int. J. Theor. Phys., 2024, 63, 306. doi: 10.1007/s10773-024-05829-y [11] L. Hu, Y. T. Gao, T. T. Jia, et al., Bilinear forms, N-soliton solutions, breathers and lumps for a (2+1)-dimensional generalized breaking soliton system, Modern Phys. Lett. B, 2022, 36(15), 2250033. doi: 10.1142/S0217984922500336 [12] X. R. Hu, S. N. Lin and L. Wang, Integrability, multiple-cosh, lumps and lump-soliton solutions to a (2+1)-dimensional generalized breaking soliton equation, Commun. Nonlinear Sci. Numer. Simulat., 2020, 91, 105447. doi: 10.1016/j.cnsns.2020.105447 [13] M. Iqbal, A. R. Seadawy and S. Althobaiti, Mixed soliton solutions for the (2+1)-dimensional generalized breaking soliton system via new analytical mathematical method, Results Phys., 2022, 32, 105030. doi: 10.1016/j.rinp.2021.105030 [14] W. F. Li, Y. C. Kuang, J. Manafian, et al., Multiple rogue wave, double-periodic soliton and breather wave solutions for a generalized breaking soliton system in (3+1)-dimensions, Sci. Rep., 2024, 14, 19723. doi: 10.1038/s41598-024-70523-2 [15] J. G. Liu, A. M. Wazwaz, R. F. Zhang, et al., Breather-wave, multi-wave and interaction solutions for the (3+1)-dimensional generalized breaking solution equation, J. Appl. Anal. Comput., 2022, 12(6), 2426–2440. [16] W. X. Ma, Lump solutions to the Kadomtsev-Petviashvili equation, Phys. Lett. A, 2015, 379(36), 1975–1978. doi: 10.1016/j.physleta.2015.06.061 [17] W. X. Ma, Lump waves and their dynamics of a spatial symmetric generalized KP model, Rom. Rep. Phys., 2024, 76(3), 108. [18] W. X. Ma, Soliton solutions to Sasa-Satsuma-Type modified Korteweg-De Vries equations by binary Darboux transformations, Mathematics, 2024, 12(23), 3643. doi: 10.3390/math12233643 [19] M. Niwas, S. Kumar and H. Kharbanda, Symmetry analysis, closed-form invariant solutions and dynamical wave structures of the generalized (3+1)-dimensional breaking soliton equation using optimal system of lie subalgebra, J. Ocean. Eng. Sci, 2022, 7(2), 188–201. doi: 10.1016/j.joes.2021.08.002 [20] R. Pouyanmehr, K. Hosseini, R. Ansari, et al., Different wave structures to the (2+1)-dimensional generalized bogoyavlensky-konopelchenko equation, Int. J. Appl. Comput. Math., 2019, 5, 149. doi: 10.1007/s40819-019-0730-z [21] H. U. Rehman, R. Akber, A. M. Wazwaz, et al., Analysis of Brownian motion in stochastic Schrödinger wave equation using Sardar sub-equation method, Optik, 2023, 289, 171305. doi: 10.1016/j.ijleo.2023.171305 [22] M. M. Roshid, M. Uddin, S. Boulaaras, et al., Dynamic optical soliton solutions of M-fractional modify unstable nonlinear Schrödinger equation via two analytic methods, Results Eng., 2025, 25, 103757. doi: 10.1016/j.rineng.2024.103757 [23] Y. D. Shang, Abundant explicit non-traveling wave solutions for the (2+1)-dimensional breaking soliton equation, Appl. Math. Lett., 2022, 131, 108029. doi: 10.1016/j.aml.2022.108029 [24] A. Silem and J. Lin, Exact solutions for a variable-coefficients nonisospectral nonlinear schrödinger equation via wronskian technique, Appl. Math. Lett., 2023, 135, 108397. doi: 10.1016/j.aml.2022.108397 [25] C. J. Wang, Z. D. Dai and L. Liang, Exact three-wave solution for higher dimensional KdV-type equation, Appl. Math. Comput., 2010, 216(2), 501–505. [26] A. M. Wazwaz. A new integrable (2+1)-dimensional generalized breaking soliton equation: N-soliton solutions and traveling wave solutions, Commun. Theor. Phys., 2016, 66, 385–388. doi: 10.1088/0253-6102/66/4/385 [27] G. Q. Xu, Integrability of a (2+1)-dimensional generalized breaking soliton equation, Appl. Math. Lett., 2015, 50, 16–22. doi: 10.1016/j.aml.2015.05.015 [28] X. W. Yan, S. F. Tian, M. J. Dong, et al., Characteristics of solitary wave, homoclinic breather wave and rogue wave solutions in a (2+1)-dimensional generalized breaking soliton equation, Comput. Math. Appl., 2018, 76(1), 179–186. doi: 10.1016/j.camwa.2018.04.013 [29] S. Yasin, A. Khan, S. Ahmad and M. S. Osman, New exact solutions of (3+1)-dimensional modified KdV-Zakharov-Kuznetsov equation by Sardar-subequation method, Opt. Quantum Electron., 2024, 56, 1163. doi: 10.1007/s11082-024-07073-4 [30] R. F. Zhang, M. C. Li, J. Y. Gan, et al., Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method, Chaos, Soliton. Fract., 2022, 154, 111692. doi: 10.1016/j.chaos.2021.111692 -
-
Figures(7)
Export File
Citation
Xiaoxiao Zheng, Xiaolin Si, Yanxiao Lu. NEW TRAVELING WAVE SOLUTIONS OF THE (3+1)-DIMENSIONAL GENERALIZED BREAKING SOLITON EQUATION[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 3045-3066. doi: 10.11948/20240520
Format
Content
DownLoad:
-
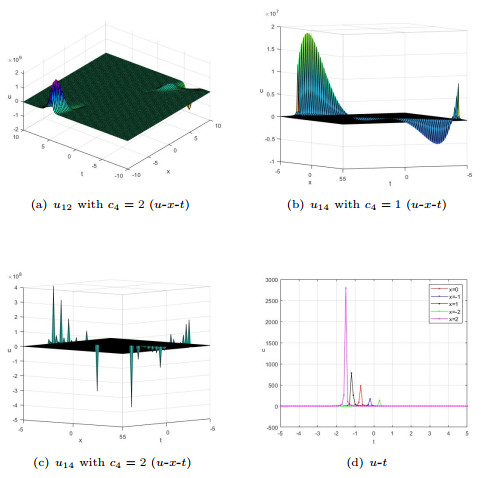
Figure 1.
$ u_{2} $ $ a_{3}=a_{4}=a_{5}=1 $ $ y=z=0 $ $ k_{3}=2 $ $ k_{4}=1 $ $ c_{3}=d_{3}=1 $ $ c_{4}=d_{4}=2 $ -
Figure 2.
hyperbolic function solutions
$ u_{5} $ $ a_{3}=a_{4}=a_{5}=1 $ $ m_{3}=m_{4}=-2 $ $ c_{4}=1 $ $ d_{3}=d_{4}=0 $ $ x=y=0 $ -
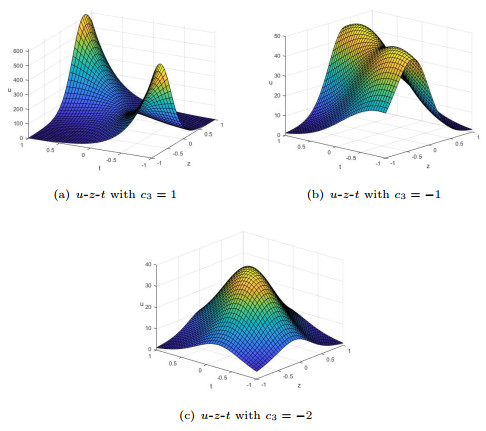
Figure 3.
$ u_{6} $ $ a_{3}=a_{4}=a_{5}=1 $ $ y=z=0 $ $ k_{3}=k_{4}=1 $ $ c_{3}=2 $ $ c_{4}=1 $ $ d_{3}=d_{4}=1 $ -
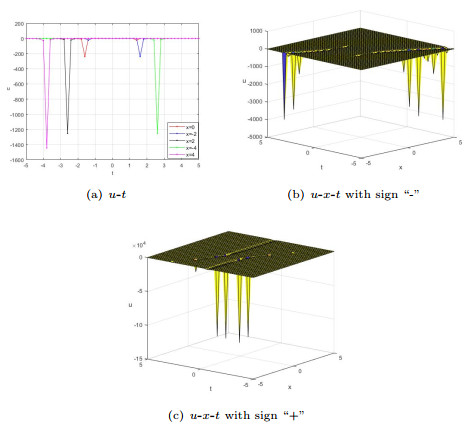
Figure 4.
$a_{2}=a_{4}=a_{5}=k_{2}=k_{4}=c_{2}=d_{2}=d_{4}=1$, $x=y=0$.
-
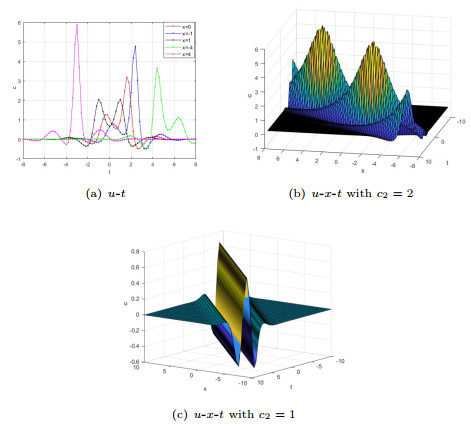
Figure 5.
$u_{40}$ as $a_{2}=1$, $a_{3}=2$, $k_{2}=k_{3}=c_{3}=1$, $d_{2}=d_{3}=-1$, $y=z=0$.
-
Figure 6.
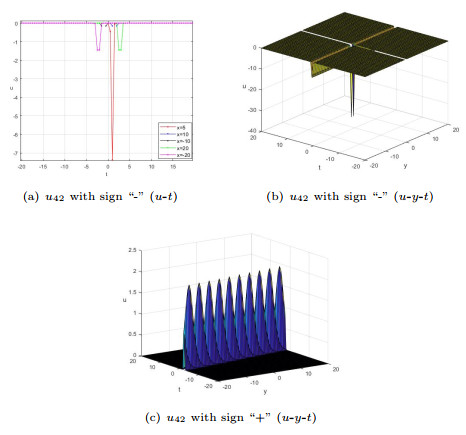
$ a_{4}=k_{3}=k_{4}=-l_{3}=d_{3}=d_{4}=1 $ $ c_{3}=c_{4}=-4 $ $ a_{3}=l_{4}=2 $ $ x=z=0 $ -
Figure 7.
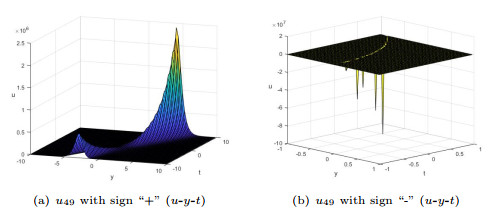
$u_{49}$ as $a_{2}=a_{3}=a_{4}=1$, $k_{3}=1$, $c_{3}=1$, $l_{3}=-1$, $l_{2}=l_{4}=-\frac{1}{2}$, $x=z=0$.