| Citation: | Yunzhe Zhang, Youhui Su, Yongzhen Yun. EXISTENCE AND STABILITY OF SOLUTIONS FOR HADAMARD TYPE FRACTIONAL DIFFERENTIAL SYSTEM ON BENZENE GRAPHS[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 3067-3094. doi: 10.11948/20240544 |
EXISTENCE AND STABILITY OF SOLUTIONS FOR HADAMARD TYPE FRACTIONAL DIFFERENTIAL SYSTEM ON BENZENE GRAPHS
-
Abstract
This paper is mainly concerned with the existence of solutions for a class of Hadamard type fractional differential systems on benzene graphs, and the Hyers-Ulam stability of the systems is also proved. Furthermore, an example is presented on a formic acid graph to demonstrate the applicability of the conclusions obtained. The interesting of this paper lies in the integration of fractional differential equations with graph theory, utilizing the formic acid graph as a specific case for numerical simulation, and providing an approximate solution graph after iterations.
-

-
References
[1] A. Z. Abdian, A. Behmaram and G. H. Fath-Tabar, Graphs determined by signless Laplacian Spectra, Akce. Int. J. Graphs. Co., 2020, 17(1), 45–50. doi: 10.1016/j.akcej.2018.06.009 [2] B. Ahmad, M. Alghanmi, A. Alsaedi, et al., Existence and uniqueness results for a nonlinear coupled system involving Caputo fractional derivatives with a new kind of coupled boundary conditions, Appl. Math. Lett., 2021, 116, 107018. doi: 10.1016/j.aml.2021.107018 [3] B. Ahmad, A. Alsaedi, S. K. Ntouyas, et al., Hadamard-Type Fractional Differential Equations, Inclusions and Inequalities, Springer, Switzerland, 2017. [4] Y. Cui, W. Ma, et. al, New uniqueness results for boundary value problem of fractional differential equation, Nonlinear. Anal-Model., 2018, 23(1), 31–39. doi: 10.15388/NA.2018.1.3 [5] L. Debnath, Fractional integrals and fractional differential equations in fluid mechanics, Frac. Calc. Appl. Anal., 2003, 6, 119155. [6] M. Faieghi, S. Kuntanapreeda, H. Delavari, et al., LMI based stabilization of a class of fractional order chaotic systems, Nonlinear. Dynam., 2013, 72(1), 301–309. [7] D. G. Gordeziani, M. Kupreishvli, H. V. Meladze, et al., On the solution of boundary value problem for differential equations given in graphs, Appl. Math. Lett., 2008, 13, 80–91. [8] J. R. Graef, L. Kong and M. Wang, Existence and uniqueness of solutions for a fractional boundary value problem on a graph, Fract. Calc. Appl. Anal., 2014, 17(2), 499–510. doi: 10.2478/s13540-014-0182-4 [9] J. Klafter, S. C. Lim and R. Metzler, Fractional Dynamics in Physics, World Scientific, Singapore, 2011. [10] V. Lakshmikanthan and A. S. Vatsala, Basic theory of fractional differential equations, Nonlinear. Anal., 2008, 69, 267–782. [11] A. Mahdy, M. S. Mohamed, K. A. Gepreel, et al., Dynamical characteristics and signal flow graph of nonlinear fractional smoking mathematical model, Chaos Soliton Fract., 2020, 141, 110308. doi: 10.1016/j.chaos.2020.110308 [12] V. Mehandiratta, M. Mehra and G. Leugering, Existence and uniqueness results for a nonlinear Caputo fractional boundary value problem on a star graphs, J. Math. Anal. Appl., 2019, 477(2), 1243–1264. doi: 10.1016/j.jmaa.2019.05.011 [13] R. Metzler and J. Klafter, Boundary value problems for fractional diffusion equations, Phys A., 2000, 278(1–2), 107–125. doi: 10.1016/S0378-4371(99)00503-8 [14] J. Nan, W. Hu, Y. Su, et al., Existence and stability of solutions for a coupled hadamard type sequence fractional differential system on glucose graphs, J. Appl. Anal. Comput., 2024, 14(2), 911–946. [15] V. Pivovarchik, Inverse problem for the Sturm-Liouville equation on a starshaped graph, Math. Nachr., 2007, 280(13), 1595–1619. [16] S. Z. Rida, A. M. A. El-Sayed and A. A. M. Arafa, Effect of bacterial memory dependent growth by using fractional derivatives reaction diffusion chemotactic model, J. Stat. Phys., 2010, 140(4), 797–811. doi: 10.1007/s10955-010-0007-8 [17] N. A. Sheikh, M. Jamil, D. Ching, et al., A generalized model for quantitative analysis of sediments loss: A Caputo time fractional model, J. King. Saud. Univ. Sci., 2020, 33(1), 101179. [18] A. Sun, Y. Su and Q. Yuan, Existence of solutions to fractional differential equations with fractional order derivative terms, J. Appl. Anal. Comput., 2021, 11(1), 486–520. [19] W. Sun, Y. Su, et al., Exsitence and simulation of positive solutions for m-point fractional differential equations with derivative terms, Open. Math., 2021, 19(1), 1820–1846. doi: 10.1515/math-2021-0131 [20] W. Sun, Y. Su and X. Han, Existence of solutions for a coupled system of Caputo-Hadamard fractional differential equations with p-laplacian operator, J. Appl. Anal. Comput., 2022, 12(5), 1885–1900. [21] J. Tariboon, S. K. Ntouyas, S. Asawasamrit, et al., Positive solutions for Hadamard differential systems with fractional integral conditions on an unbounded domain, Open. Math., 2017, 15(1), 645–666. doi: 10.1515/math-2017-0057 [22] D. Tripathil, S. Pandey and S. Das, Peristaltic flow of viscoelastic fluid with fractional maxwell model through a channel, Appl. Math. Comput., 2010, 215, 3645–3654. [23] A. Turab and W. Sintunavarat, The novel existence results of solutions for a nonlinear fractional boundary value problem on the ethane graph, Alex. Eng. J., 2021, 60(6), 5365–5374. doi: 10.1016/j.aej.2021.04.020 [24] J. R. Wang, Y. Zhou and M. Medve, Existence and stability of fractional differential equations with Hadamard derivative, Topol. Method. Non. Anal., 2013, 41(1), 113–133. [25] W. Zhang and W. Liu, Existence and Ulam's type stability results for a class of fractional boundary value problems on a star graphs, Math. Method. Appl. Sci., 2020, 43, 8568–8594. doi: 10.1002/mma.6516 [26] Y. Zhang, Y. Su and Y. Yun, Exsitence and stability of solutions for Hadamard type fractional differential systems with p-Laplacian operators on benzoic acid garphs, AIMS Math., 2025, 10(4), 7767–7794. doi: 10.3934/math.2025356 -
-
-
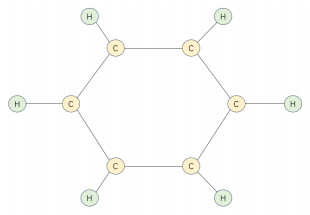
Figure 1.
Molecular structure of benzene.
-
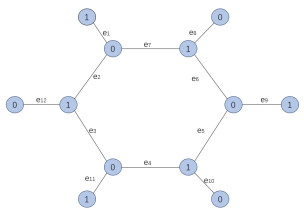
Figure 2.
Benzene graphs with vertices 0 or 1.
-
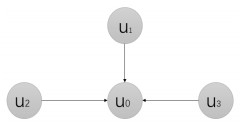
Figure 3.
A sketch of
$ C_{2}H_{2}0 $ -
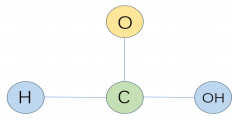
Figure 4.
Formic acid graph with labeled vertices.
-
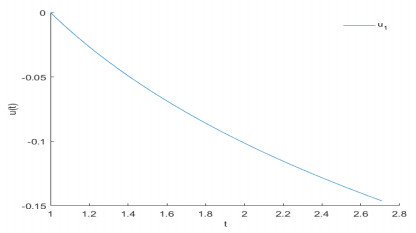
Figure 5.
Approximate solution of
$ u_{1} $ -
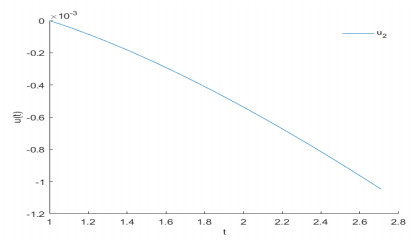
Figure 6.
Approximate solution of
$ u_{2} $ -
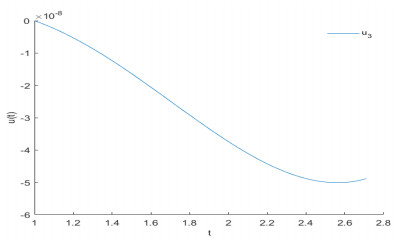
Figure 7.
Approximate solution of
$ u_{3} $




 DownLoad:
DownLoad: