| Citation: | Yue Liu, Jing Pang, Yajun Du, Tianle Yin. MODIFIED HOMOTOPY PERTURBATION METHODS FOR SOLVING PARTIAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2853-2865. doi: 10.11948/20250011 |
MODIFIED HOMOTOPY PERTURBATION METHODS FOR SOLVING PARTIAL DIFFERENTIAL EQUATIONS
-
Abstract
Homotopy perturbation method can be widely accepted for approximating or accurately solving nonlinear differential equations due to its generality and ease of use. Rational homotopy perturbation method and Rational biparameter homotopy perturbation method are two extensions of homotopy perturbation method which can improve the accuracy of the solution. In this paper, the algorithm steps of these two derived methods are introduced, meanwhile, the approximate solutions of Burgers equation and Gardner equation are obtained. Absolute errors of these two methods in solving partial differential equations are calculated and described to verify the effectiveness of the methods.
-

-
References
[1] K. S. Albalawi, B. S. Alkahtani, A. Kumar and P. Goswami, Numerical solution of time-fractional Emden-Fowler-type equations using the Rational homotopy perturbation method, Symmetry-Basel, 2023, 15(2), 258–258. doi: 10.3390/sym15020258 [2] A. M. Alqahtani, Solution of the generalized Burgers equation using homotopy perturbation method with general fractional derivative, Symmetry-Base, 2023, 15(3), 634–634. doi: 10.3390/sym15030634 [3] A. Arafa and G. Elmahdy, Application of residual power series method to fractional coupled physical equations arising in fluids flow, International Journal of Differential Equations, 2018, 1–10. [4] J. Biazar, M. A. Asadi and F. Salehi, Rational homotopy perturbation method for solving stiff systems of ordinary differential equations, Applied Mathematical Modelling, 2015, 39(3–4), 1291–1299. [5] J. Biazar and H. Ghazvini, Exact solutions for nonlinear Burgers' equation by homotopy perturbation method, Numerical Methods for Partial Differential Equations, 2009, 25(4), 833–842. doi: 10.1002/num.20376 [6] J. M. Burger, A Mathematical Model Illustrating the Theory of Turbulence, Academic Press, New York, 1948. [7] C. Cesarano, Y. Massoun, A. Said and M. E. Talbi, Analytic study of coupled Burgers' equation, Mathematics, 2023, 11(9), 2071–2071. doi: 10.3390/math11092071 [8] S. Chen, Comparison and Application Research Based on Homotopy Perturbation Derivation Method, Ph.M. University of Science and Technology Liaoning, 2022. [9] Y. J. Du, T. L. Yin and J. Pang, The exact solutions of Schrödinger-Hirota equation based on the auxiliary equation method, Optical and Quantum Electronics, 2024, 56(5). [10] J. H. He, Homotopy perturbation technique, Computer Methods in Applied Mechanics and Engineering, 1999, 178(3–4), 257–262. [11] M. Inc, On numerical solution of Burgers' equation by homotopy analysis method, Physics Letters A, 2008, 372(4), 356–360. doi: 10.1016/j.physleta.2007.07.057 [12] O. S. Iyiola and O. G. Olayinka, Analytical solutions of time-fractional models for homogeneous Gardner equation and non-homogeneous differential equations, Ain Shams Engineering Jouanal, 2014, 5(3), 999–1004. doi: 10.1016/j.asej.2014.03.014 [13] M. Kapoor, Exact solution of coupled 1D non-linear Burgers' equation by using homotopy perturbation method (HPM): A review, Journal of Physics Communications, 2020, 4(9), 1–6. [14] M. Kumar and D. V. Tanwar, On Lie symmetries and invariant solutions of (2+1)-dimensional Gardner equation, Communications in Nonlinear Science and Numerical Simulation, 2019, 69, 45–57. doi: 10.1016/j.cnsns.2018.09.009 [15] H. Vázquez-Leal, Rational homotopy perturbation method, Journal of Applied Mathematics, 2012, 1–14. [16] H. Vázquez-Leal, U. Filobello-Niño, R. Castañeda-Sheissa, L. Hernández-Martínez and A. Sarmiento-Reyes, Modified HPMs inspired by homotopy continuation methods, Mathematical Problems in Engineering, 2012, 1–19. [17] H. Vázquez-Leal, A. Sarmiento-Reyes, Y. Khan, U. Filobello-Nino and A. Diaz-Sanchez, Rational biparameter homotopy perturbation method and Laplace-Pade coupled version, Journal of Applied Mathematics, 2012, 1–21. [18] H. R. Li, Research based on Rational homotopy perturbation method for solving optimal control problems, Ph.M. University of Science and Technology Liaoning, 2021. [19] W. W. Mohammed, C. Cesarano, N. I. Alqsair and R. Sidaoui, The impact of Brownian motion on the optical solutions of the stochastic ultra-short pulses mathematical model, Alexandria Engineering Journal, 2024, 101, 186–192. doi: 10.1016/j.aej.2024.05.054 [20] W. W. Mohammed, C. Cesarano, A. A. Elmandouh, I. Alqsair, R. Sidaoui and H. W. Alshammari, Abundant optical soliton solutions for the stochastic fractional fokas system using bifurcation analysis, Physica Scripta, 2024, 99(4), 045233. [21] D. G. Prakasha, P. Veeresha and H. M. Baskonus, Two novel computational techniques for fractional Gardner and Cahn-Hilliard equations, Computationsl and Mathematical Methods, 2019, 1(2). [22] B. Ren, Symmetry reduction related with nonlocal symmetry for Gardner equation, Communications in Nonlinear Science and Numerical Simulation, 2017, 42, 456–463. [23] P. Sripacharasakullert, W. Sawangtong and P. Sawangtong, An approximate analytical solution of the fractional multi-dimensional Burgers equation by the homotopy perturbation method, Advances in Difference Equations, 2019, 2019(1), 1–12. [24] S. K. Vanani and F. Soleymani, Application of the homotopy perturbation method to the Burgers equation with delay, Chinese Physics Letters, 2012, 29(3), 5–8. [25] T. L. Yin, Z. Q. Xing and J. Pang, Modified Hirota bilinear method to (3+1)-D variable coefficients generalized shallow water wave equation, Nonlinear Dynamics, 2023, 111(11), 9741–9752. [26] M. Zakarya, M. Altanji, G. AlNemer, H. A. A. El-Hamid, C. Cesarano and H. M. Rezk, Fractional reverse Coposn’s inequalities via conformable calculus on time scales, Symmetry, 2021, 13, 542. [27] J. J. Zhao, R. Zhan and Y. Xu, The analysis of operator splitting for the Gardner equation, Applied Numerical Mathematics, 2019, 144, 151–175. [28] Z. Zhao and J. Pang, Solitary wave solutions of GKP equation with (2+1) dimensional variable-coefficients in dynamic systems, Chaos, Solitons and Fractals: X, 2022, 8. -
-
-
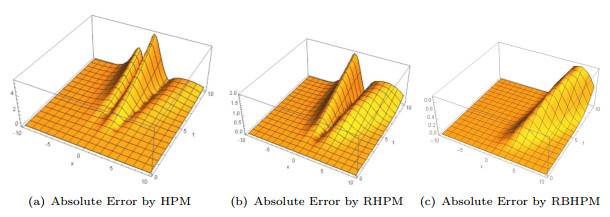
Figure 1.
Error diagram of three approximate solutions and the exact solution of Burgers equation.
-
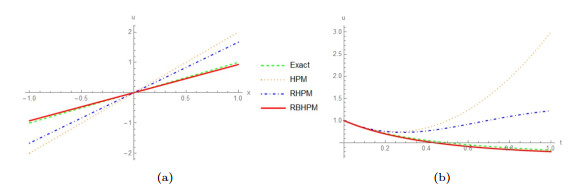
Figure 2.
2D plots of three approximate solutions and the exact solution of Burgers equation.
-
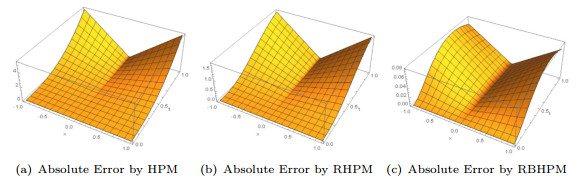
Figure 3.
Error diagram of three approximate solutions and the exact solution of Gardner equation.
-
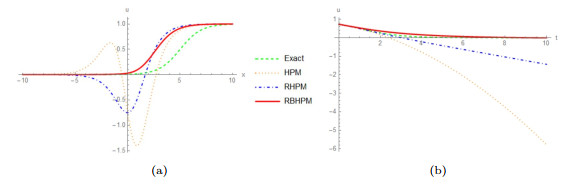
Figure 4.
2D plots of three approximate solutions and the exact solution of Gardner equation.




 DownLoad:
DownLoad: