| Citation: |
Ercan Balci. A FRACTIONAL PREDATOR-PREY MODEL WITH ALLEE EFFECT AND CONSTRUCTIVE IMPACT ON PREY CARRYING CAPACITY[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3414-3432. doi: 10.11948/20250052
|
A FRACTIONAL PREDATOR-PREY MODEL WITH ALLEE EFFECT AND CONSTRUCTIVE IMPACT ON PREY CARRYING CAPACITY
-
Abstract
This paper explores a prey-predator model that incorporates several biological phenomena, with a focus on the positive feedback that certain prey species have on their own carrying capacity. Traditional models treat carrying capacity as a constant; however, this study assumes a variable carrying capacity influenced by the prey population. To account for the memory effect and hereditary properties within biological systems, we employ fractional differential equations using the Caputo fractional derivative. Additionally, we incorporate the Allee effect, which plays a critical role in population dynamics, especially at low population densities. Through numerical analysis, the model's stability and dynamic behavior are examined, providing insights into species coexistence, population cycles, and extinction risks. This framework aims to enrich existing models and offer a more comprehensive understanding of prey-predator interactions with prey species impacting their carrying capacity.
-
Keywords:
- Prey-predator /
- carrying capacity /
- Allee effect /
- Caputo fractional derivative /
- Hopf bifurcation
-
-
References
[1] P. A. Abrams and J. D. Roth, The effects of enrichment of three-species food chains with nonlinear functional responses, Ecology, 1994, 75(4), 1118–1130. doi: 10.2307/1939435 [2] B. G. Bergman and J. K. Bump, Revisiting the role of aquatic plants in beaver habitat selection, The American Midland Naturalist, 2018, 179(2), 222–246. doi: 10.1674/0003-0031-179.2.222 [3] D. Burchsted, M. Daniels, R. Thorson and J. Vokoun, The river discontinuum: Applying beaver modifications to baseline conditions for restoration of forested headwaters, BioScience, 2010, 60(11), 908–922. doi: 10.1525/bio.2010.60.11.7 [4] M. Çiçek, C. Yakar and B. Oğur, Stability, boundedness, and lagrange stability of fractional differential equations with initial time difference, The Scientific World Journal, 2014, 2014. [5] Q. Dai, Exploration of bifurcation and stability in a class of fractional-order super-double-ring neural network with two shared neurons and multiple delays, Chaos, Solitons & Fractals, 2023, 168, 113185. [6] S. Das, S. K. Mahato, A. Mondal and E. Kaslik, Emergence of diverse dynamical responses in a fractional-order slow–fast pest–predator model, Nonlinear Dynamics, 2023, 111(9), 8821–8836. doi: 10.1007/s11071-023-08292-2 [7] K. Diethelm, N. J. Ford and A. D. Freed, A predictor-corrector approach for the numerical solution of fractional differential equations, Nonlinear Dynamics, 2002, 29, 3–22. doi: 10.1023/A:1016592219341 [8] M. Farman, C. Xu, P. Abbas, et al., Stability and chemical modeling of quantifying disparities in atmospheric analysis with sustainable fractal fractional approach, Communications in Nonlinear Science and Numerical Simulation, 2025, 142, 108525. doi: 10.1016/j.cnsns.2024.108525 [9] T. D. Gable, S. M. Johnson-Bice, A. T. Homkes, et al., Outsized effect of predation: Wolves alter wetland creation and recolonization by killing ecosystem engineers, Science Advances, 2020, 6(46), eabc5439. doi: 10.1126/sciadv.abc5439 [10] Y. Galviz, G. M. Souza and U. Lüttge, The biological concept of stress revisited: Relations of stress and memory of plants as a matter of space–time, Theoretical and Experimental Plant Physiology, 2022, 34(2), 239–264. doi: 10.1007/s40626-022-00245-1 [11] R. Garrappa, On linear stability of predictor–corrector algorithms for fractional differential equations, International Journal of Computer Mathematics, 2010, 87(10), 2281–2290. doi: 10.1080/00207160802624331 [12] B. Ghosh, Fractional order modeling of ecological and epidemiological systems: Ambiguities and challenges, The Journal of Analysis, 2024, 1–26. [13] P. H. Leslie, A stochastic model for studying the properties of certain biological systems by numerical methods, Biometrika, 1958, 45(1–2), 16–31. doi: 10.1093/biomet/45.1-2.16 [14] H. Li and Y. Tian, Dynamic behavior analysis of a feedback control predator-prey model with exponential fear effect and hassell-varley functional response, Journal of the Franklin Institute, 2023, 360(4), 3479–3498. doi: 10.1016/j.jfranklin.2022.11.030 [15] P. Li, R. Gao, C. Xu, et al., Dynamics exploration for a fractional-order delayed zooplankton–phytoplankton system, Chaos, Solitons & Fractals, 2023, 166, 112975. [16] P. Li, C. Xu, M. Farman, et al., Qualitative and stability analysis with lyapunov function of emotion panic spreading model insight of fractional operator, Fractals, 2024, 32(02), 2440011. [17] Y. Li, Y. Chen and I. Podlubny, Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized mittag–leffler stability, Computers & Mathematics with Applications, 2010, 59(5), 1810–1821. [18] Y. Li, Z. Liu and Z. Zhang, Hopf bifurcation for an age-structured predator–prey model with crowley–martin functional response and two delays, Qualitative Theory of Dynamical Systems, 2023, 22(2), 66. doi: 10.1007/s12346-023-00765-4 [19] P. Majumdar, B. Mondal, S. Debnath and U. Ghosh, Controlling of periodicity and chaos in a three dimensional prey predator model introducing the memory effect, Chaos, Solitons & Fractals, 2022, 164, 112585. [20] H. E. Milligan and M. M. Humphries, The importance of aquatic vegetation in beaver diets and the seasonal and habitat specificity of aquatic-terrestrial ecosystem linkages in a subarctic environment, Oikos, 2010, 119(12), 1877–1886. doi: 10.1111/j.1600-0706.2010.18160.x [21] W. J. Mitsch, What is ecological engineering?, Ecological Engineering, 2012, 45, 5–12. doi: 10.1016/j.ecoleng.2012.04.013 [22] D. Müller-Schwarze, The Beaver: Natural History of a Wetlands Engineer, Cornell University Press, 2017. [23] S. Pal, A. Gupta, A. Misra and B. Dubey, Complex dynamics of a predator–prey system with fear and memory in the presence of two discrete delays, The European Physical Journal Plus, 2023, 138(11), 984. doi: 10.1140/epjp/s13360-023-04614-w [24] N. Pati and B. Ghosh, Delayed carrying capacity induced subcritical and supercritical hopf bifurcations in a predator–prey system, Mathematics and Computers in Simulation, 2022, 195, 171–196. doi: 10.1016/j.matcom.2022.01.008 [25] I. Petráš, Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation, Springer Science & Business Media, 2011. [26] F. Rosell, O. Bozser, P. Collen and H. Parker, Ecological impact of beavers castor fiber and castor canadensis and their ability to modify ecosystems, Mammal review, 2005, 35(3–4), 248–276. doi: 10.1111/j.1365-2907.2005.00067.x [27] M. L. Rosenzweig, Paradox of enrichment: Destabilization of exploitation ecosystems in ecological time, Science, 1971, 171(3969), 385–387. doi: 10.1126/science.171.3969.385 [28] D. Roy and B. Ghosh, Dimensionally homogeneous fractional order rosenzweig–macarthur model: A new perspective of paradox of enrichment and harvesting, Nonlinear Dynamics, 2024, 112(20), 18137–18161. doi: 10.1007/s11071-024-09959-0 [29] H. M. Safuan, H. S. Sidhu, Z. Jovanoski and I. N. Towers, A two-species predator-prey model in an environment enriched by a biotic resource, Anziam J., 2012, 54, C768–C787. [30] J. Sharrock and J. C. Sun, Innate immunological memory: From plants to animals, Current Opinion in Immunology, 2020, 62, 69–78. doi: 10.1016/j.coi.2019.12.001 [31] J. J. Shepherd and L. Stojkov, The logistic population model with slowly varying carrying capacity, Anziam J., 2005, 47, C492–C506. [32] J. Wang, J. Liu and R. Zhang, Stability and bifurcation analysis for a fractional-order cancer model with two delays, Chaos, Solitons & Fractals, 2023, 173, 113732. [33] R. Watson, I. Baste, A. Larigauderie, et al., Summary for policymakers of the global assessment report on biodiversity and ecosystem services of the intergovernmental science-policy platform on biodiversity and ecosystem services, IPBES Secretariat: Bonn, Germany, 2019, 22–47. [34] C. Xu, M. Farman, Y. Pang, et al., Mathematical analysis and dynamical transmission of seirisr model with different infection stages by using fractional operator, International Journal of Biomathematics, 2024, 2450151. [35] C. Xu, M. Farman and A. Shehzad, Analysis and chaotic behavior of a fish farming model with singular and non-singular kernel, International Journal of Biomathematics, 2023, 2350105. [36] C. Xu, M. Farman, A. Shehzad and K. Sooppy Nisar, Modeling and ulam–hyers stability analysis of oleic acid epoxidation by using a fractional-order kinetic model, Mathematical Methods in the Applied Sciences, 2025, 48(3), 3726–3747. doi: 10.1002/mma.10510 [37] C. Xu, M. Liaob, M. Farman and A. Shehzade, Hydrogenolysis of glycerol by heterogeneous catalysis: Fractional order kinetic model with analysis, MATCH Commun. Math. Comput. Chem., 2024, 91(3), 635–664. doi: 10.46793/match.91-3.635X [38] V. I. Yukalov, E. Yukalova and D. Sornette, Punctuated evolution due to delayed carrying capacity, Physica D: Nonlinear Phenomena, 2009, 238(17), 1752–1767. doi: 10.1016/j.physd.2009.05.011 -
-
Figures(10) / Tables(1)
Export File
Citation
Ercan Balci. A FRACTIONAL PREDATOR-PREY MODEL WITH ALLEE EFFECT AND CONSTRUCTIVE IMPACT ON PREY CARRYING CAPACITY[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3414-3432. doi: 10.11948/20250052
Format
Content
DownLoad:
-
Figure 1.
Phase diagrams for different inital conditions with
$ \zeta=0.80 ; $ $ K=1, \, d=0.12 $ $ K=2, \, d=0.08 $ -
Figure 2.
Time series solution of the system (2.5) for different fractional order parameter.
-
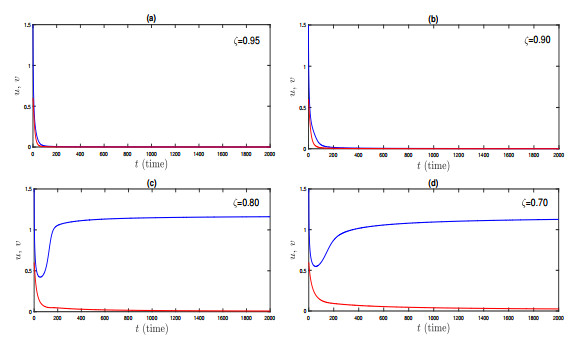
Figure 3.
Time series solution of the system (2.5) for different fractional order parameter.
-
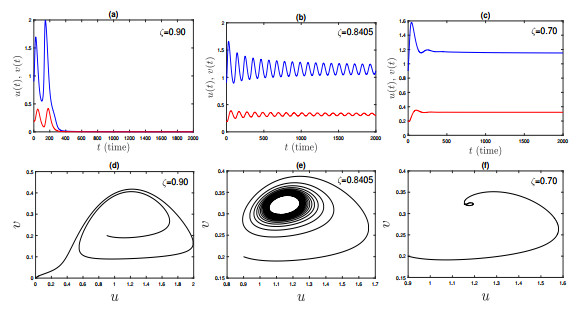
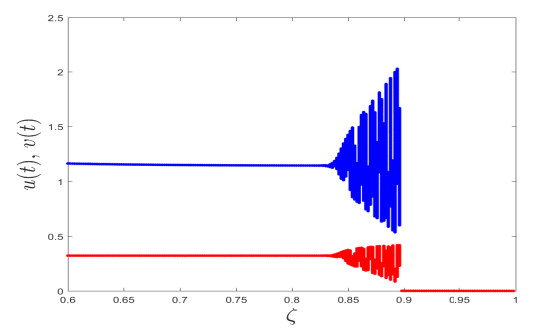
Figure 4.
Bifurcation diagrams for the system (2.5) with respect to
$ \zeta $ -
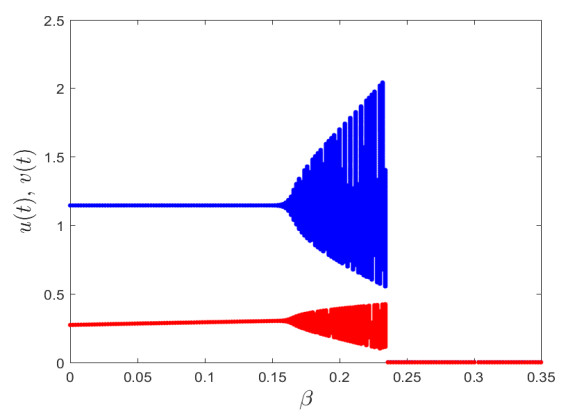
Figure 5.
Bifurcation diagrams for the system (2.5) with respect to constructive impact parameter
$ \beta $ -
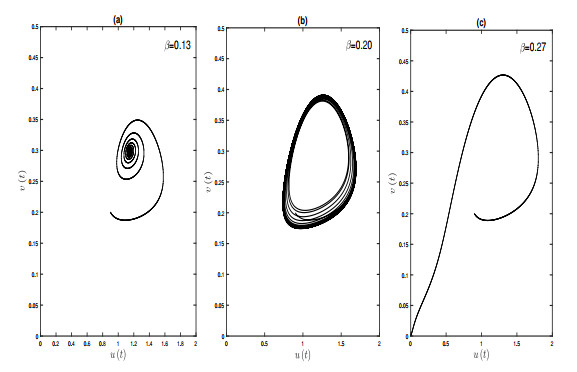
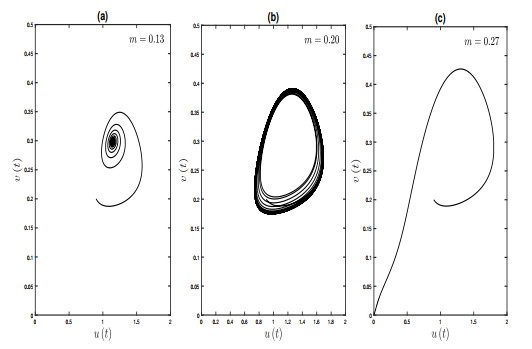
Figure 6.
Phase diagrams for three different values of the constructive impact parameter
$ \beta $ -
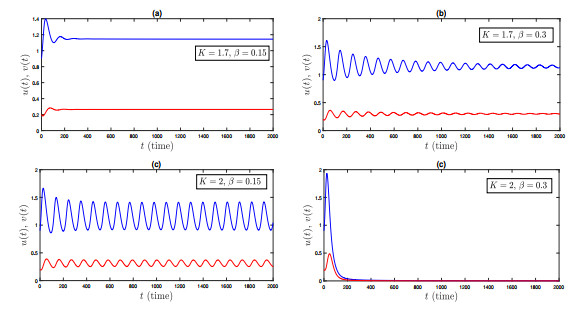
Figure 7.
Time series solution of the system (2.5) for different values of
$ K $ $ \beta $ $ \zeta=0.85 $ -
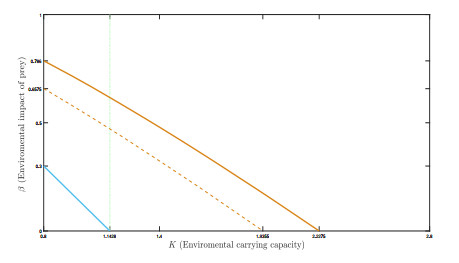
Figure 8.
The schematic bifurcation diagram of parameters
$ K $ $ \beta $ $ \zeta=0.85 $ -
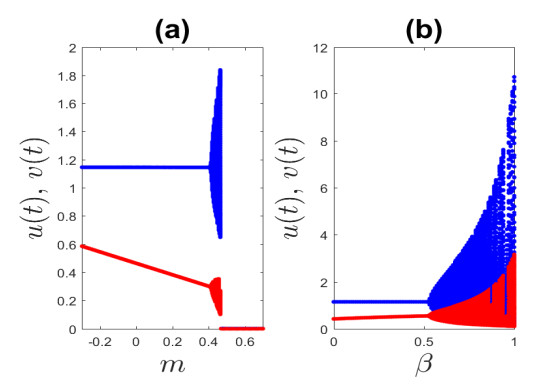
Figure 9.
(a) Bifurcation diagram with respect to Allee parameter
$ m $ $ \beta $ $ m=0 $ -
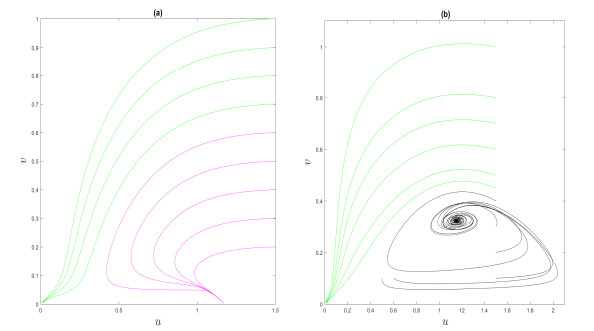
Figure 10.
Phase diagrams for three different values of the constructive impact parameter
$ \beta $